Law of Cosines Worksheets
About These 15 Worksheets
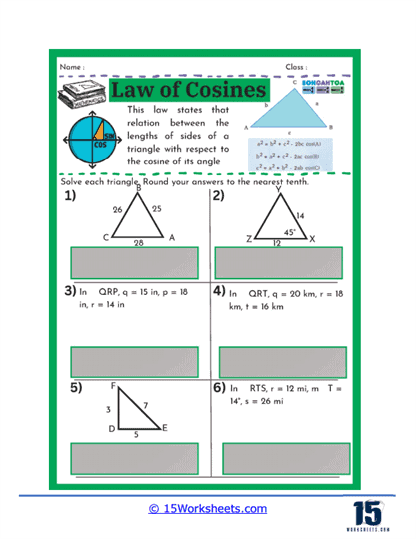
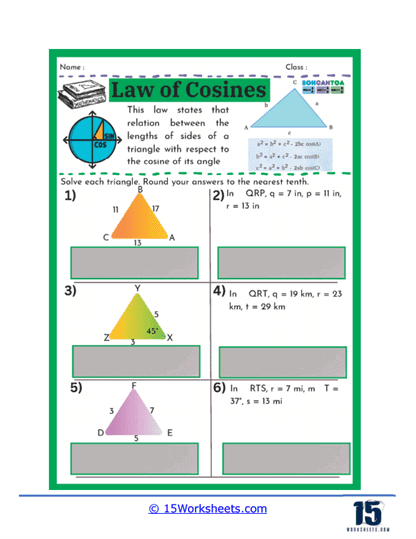
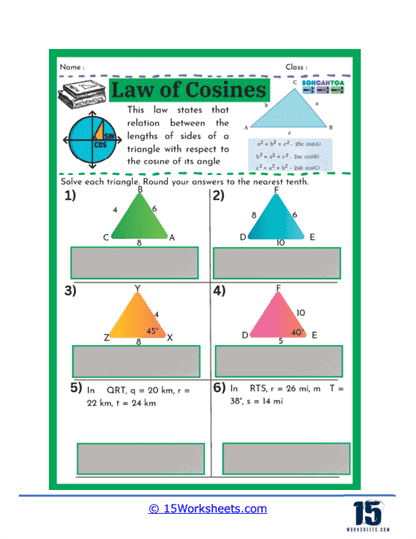
These worksheets will help students how to apply the Law of Cosines to solve various types of triangles, especially when dealing with non-right triangles. These worksheets typically present a variety of problems where students are required to calculate the lengths of sides or the measures of angles in a triangle using the Law of Cosines. This law is particularly useful in situations where the traditional Pythagorean Theorem does not apply, such as when the triangle does not have a right angle. Through these exercises, students learn how to navigate through more complex trigonometric problems, reinforcing their understanding of triangle properties and the relationships between the sides and angles.
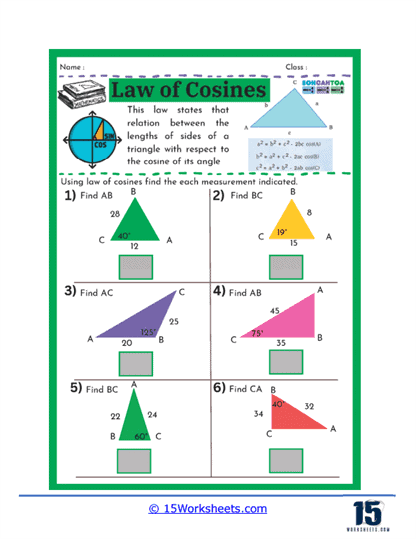
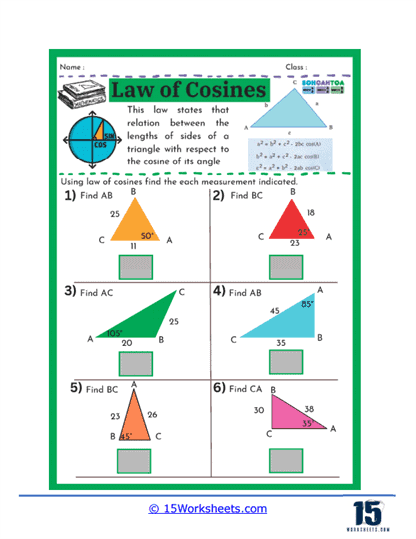
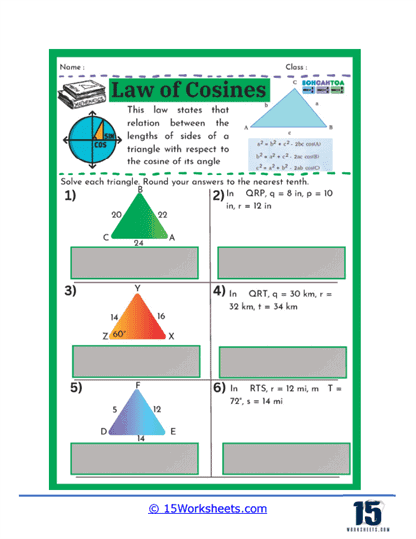
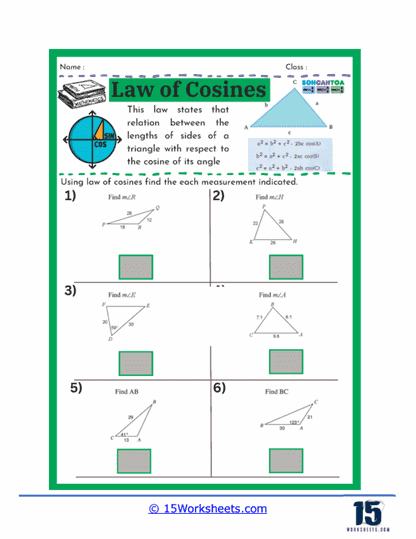
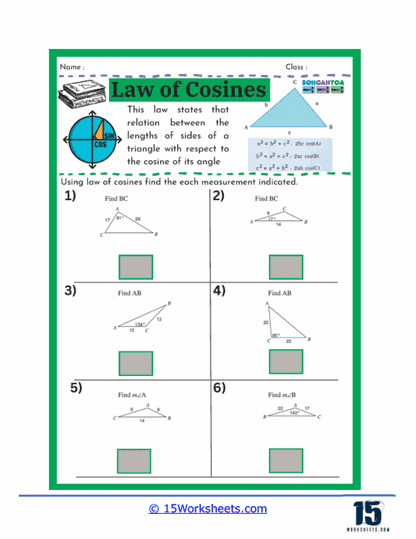
One common type of problem found on these worksheets involves giving students the measurements of two sides of a triangle and the included angle, and asking them to find the length of the third side. This kind of problem helps students practice applying the Law of Cosines formula, which relates the sides of a triangle to the cosine of one of its angles. By working through these problems, students gain confidence in their ability to manipulate the formula and solve for unknown sides, which is a critical skill in trigonometry.
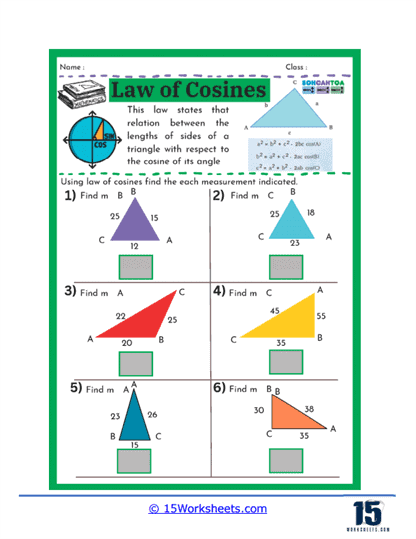
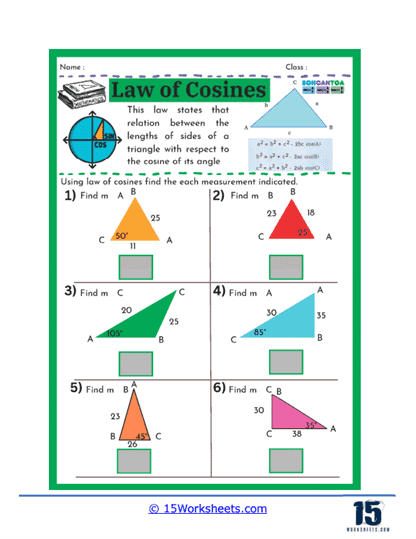
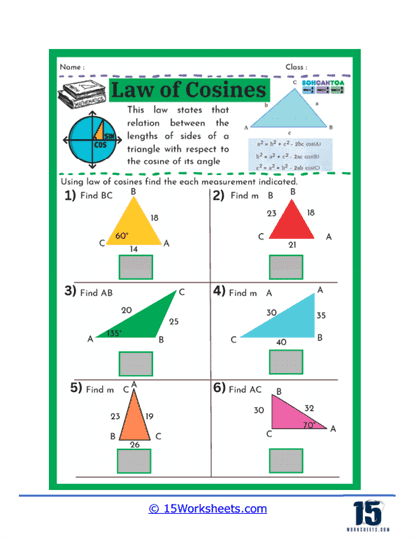
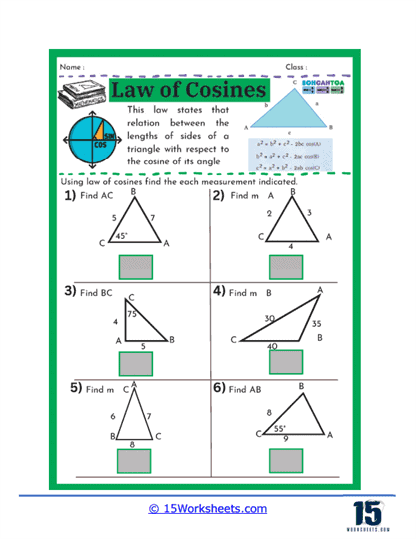
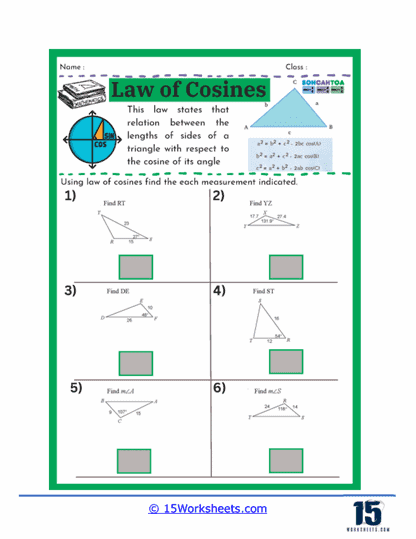
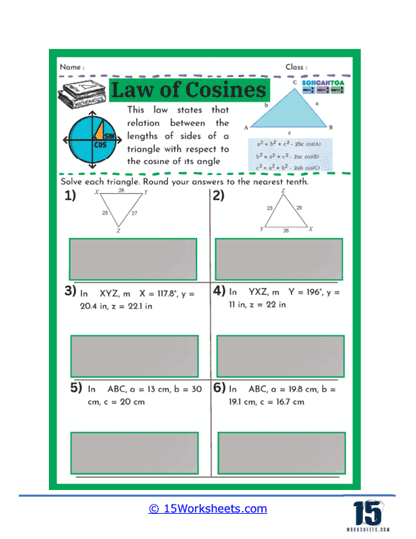
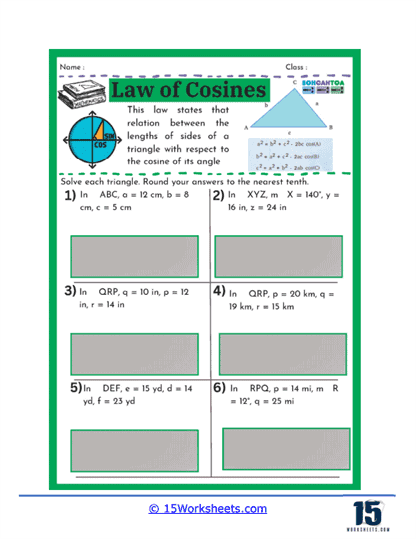
On these worksheets, you can expect to see several types of problems. First, there are problems where students are given two sides of a triangle and the angle between them (SAS scenario) and are asked to find the third side. These problems help students practice substituting known values into the Law of Cosines formula and solving for the unknown side. Another common type of problem involves finding an angle when all three sides of a triangle are known (SSS scenario). Here, students use the rearranged formula to solve for the cosine of the angle, and then use the inverse cosine function to find the angle itself.
Another type of exercise on this set of worksheets may present students with all three sides of a triangle and require them to find one of the angles. This reverse application of the Law of Cosines helps students understand how to isolate and solve for an angle when given all sides. Such problems enhance a student’s ability to understand and work with trigonometric identities, deepening their comprehension of how angles and sides interact in a triangle.
Some worksheets include word problems where students must apply the Law of Cosines to real-world scenarios. For example, a problem might describe a situation where two paths diverge from a common point and meet at another point, forming a triangle. The student might be required to calculate the distance between the starting point and the meeting point, given the lengths of the other two paths and the angle between them. These kinds of problems not only reinforce the mathematical concepts but also show students how trigonometry can be used to solve practical problems.
Other worksheets include problems that require students to decide whether to use the Law of Sines or the Law of Cosines, depending on the information given. This helps students develop critical thinking skills and a deeper understanding of when each law is applicable. Additionally, more advanced worksheets might include problems involving the ambiguous case of the Law of Sines, where the Law of Cosines can be used to resolve ambiguities.
Practicing with these worksheets can significantly enhance a student’s understanding of geometry and its applications in the real world. By working through these problems, students learn how to approach complex geometric situations and apply mathematical reasoning to find solutions. This skill is invaluable in many real-world scenarios, such as in architecture, where precise measurements are crucial for designing stable structures, or in computer graphics, where understanding the geometry of shapes is essential for creating realistic images.
These worksheets help students develop problem-solving skills that are applicable beyond mathematics. The process of analyzing a problem, determining the appropriate formula to use, and carrying out the necessary calculations requires logical thinking and attention to detail. These skills are transferable to many other disciplines, including science, technology, engineering, and even everyday decision-making.
By offering a range of problems, from basic calculations to real-world applications, these worksheets provide students with the opportunity to practice and deepen their understanding of how to solve triangles. This not only prepares them for more advanced studies in mathematics but also equips them with valuable skills for a wide range of real-world applications. Through consistent practice, students gain confidence in their ability to tackle complex geometric problems and develop a strong foundation for future learning in mathematics and related fields.