Trigonometric Ratios Worksheets
About These 15 Worksheets
These worksheets can show students how to apply the fundamental concepts of trigonometry to right-angled triangles. These worksheets focus on helping students understand and calculate the relationships between the sides and angles of a right triangle using the trigonometric ratios: sine, cosine, and tangent. Through a variety of exercises, students learn how these ratios are used to solve problems involving triangles, both in theoretical and practical contexts. The worksheets cover a wide range of topics and difficulty levels, ensuring that students build a solid foundation in trigonometry.
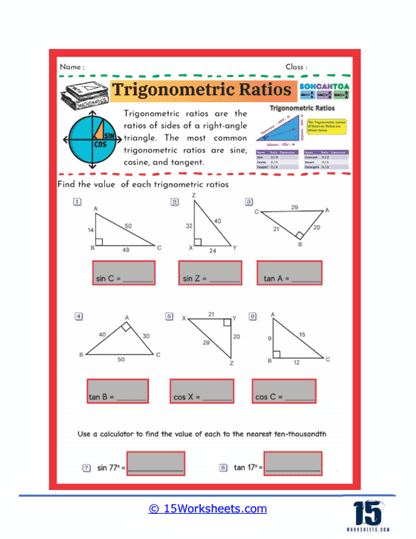
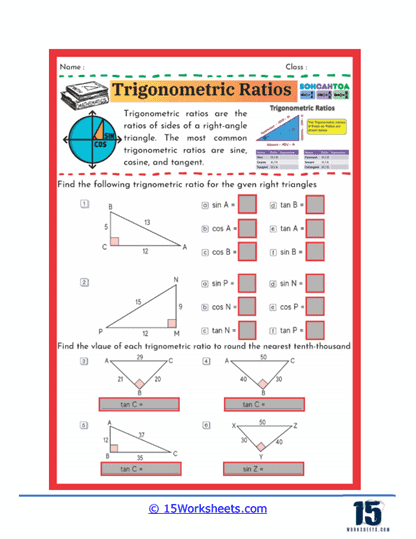
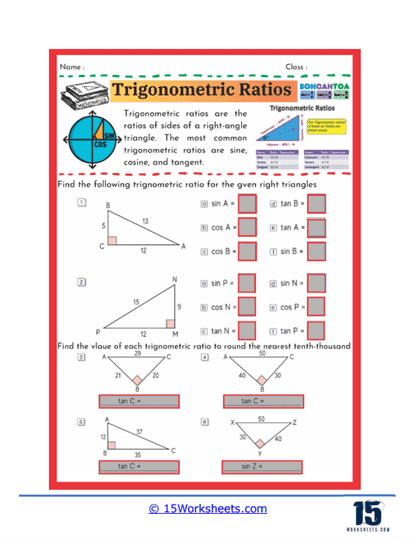
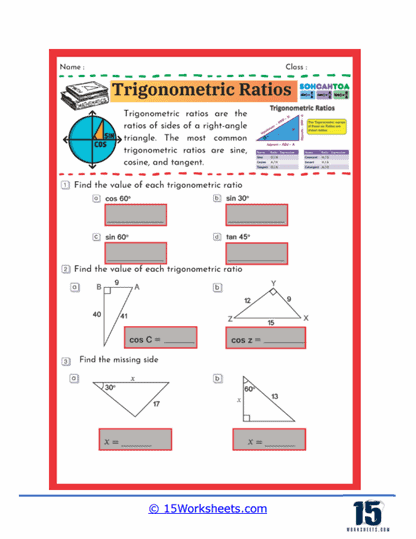
One common type of exercise found in these worksheets involves calculating the value of a specific trigonometric ratio given the sides of a right triangle. For example, students might be asked to find the sine, cosine, or tangent of a particular angle in a triangle. These problems reinforce the concept that the sine of an angle is the ratio of the opposite side to the hypotenuse, the cosine is the ratio of the adjacent side to the hypotenuse, and the tangent is the ratio of the opposite side to the adjacent side. By repeatedly solving these problems, students become familiar with these definitions and learn how to apply them in various scenarios.
Another common exercise is finding the missing side of a right triangle when given one side and one trigonometric ratio. This type of problem requires students to rearrange the trigonometric ratio equation to solve for the unknown side. These exercises help students practice algebraic manipulation while reinforcing their understanding of trigonometric relationships. For instance, if students are given the sine of an angle and the length of the hypotenuse, they can multiply the sine by the hypotenuse to find the length of the opposite side. Such problems are vital for helping students see the practical applications of trigonometry, particularly in fields like physics, engineering, and architecture.
Some worksheets also include problems where students are asked to find the value of a trigonometric ratio for angles given in degrees or radians. These exercises typically involve using a calculator to find the sine, cosine, or tangent of angles such as 30°, 45°, or 60°. Students might also be required to round their answers to a specific number of decimal places, which helps them develop precision in their calculations. This practice is crucial for students as they prepare for more advanced studies in mathematics, where exact values and accuracy are often required.
Another important type of problem found in these worksheets involves determining the measure of an angle given the sides of a triangle. In these problems, students use the inverse trigonometric functions-such as arcsine, arccosine, and arctangent-to find the angle that corresponds to a given trigonometric ratio. This type of exercise is particularly useful in real-world applications, such as navigation and surveying, where it is often necessary to determine an angle based on measured distances. By practicing these problems, students learn how to apply trigonometry to find unknown angles, an essential skill in many scientific and technical fields.
In addition to the basic sine, cosine, and tangent ratios, some worksheets introduce students to more advanced trigonometric concepts, such as the reciprocal trigonometric functions: cosecant, secant, and cotangent. These problems require students to calculate the reciprocal of the sine, cosine, or tangent of an angle, further expanding their understanding of trigonometric relationships. These exercises are often more challenging, as they require students to first calculate the primary trigonometric ratio and then find its reciprocal. This type of problem helps students develop a deeper understanding of trigonometric functions and their interrelationships.
Worksheets also include problems that require students to work with special triangles, such as 30°-60°-90° triangles and 45°-45°-90° triangles. These special triangles have specific side ratios that students can use to quickly find the trigonometric ratios without needing a calculator. By solving problems involving special triangles, students reinforce their understanding of these unique ratios and learn how to apply them to solve more complex problems. This type of problem is particularly useful for students preparing for standardized tests, where they may need to solve trigonometric problems quickly and efficiently.
Some of the worksheets in this collection integrate real-world scenarios into the problems, asking students to apply trigonometric ratios to practical situations. For example, students might be asked to calculate the height of a building or the distance across a river using trigonometry. These problems help students see the relevance of trigonometry in everyday life and demonstrate how the mathematical concepts they are learning can be applied to solve real-world problems. This type of exercise is especially engaging for students, as it allows them to connect abstract mathematical ideas to concrete situations they can relate to.
They cover a wide range of topics, from basic calculations of sine, cosine, and tangent to more advanced concepts such as inverse trigonometric functions and special triangles. These worksheets provide students with ample practice in applying trigonometric ratios to solve problems involving right triangles, both in theoretical exercises and real-world scenarios. By working through these problems, students build a solid foundation in trigonometry that will serve them well in their future studies and careers.