Reference and Coterminal Angles Worksheets
About These 15 Worksheets
Reference and coterminal angles are foundational concepts in trigonometry, essential for understanding how angles function within the unit circle and across different rotations. Worksheets focused on these concepts are designed to help students grasp the nuances of angle measurement, especially when dealing with angles that extend beyond the standard 0° to 360° range or the equivalent in radians. These worksheets typically present a variety of problems that require students to calculate either the reference angle or the coterminal angles, or sometimes both, depending on the given information. The diversity in problem types across these worksheets ensures that students gain a comprehensive understanding of these concepts, which are crucial for more advanced studies in trigonometry and calculus.
Understanding Reference Angles
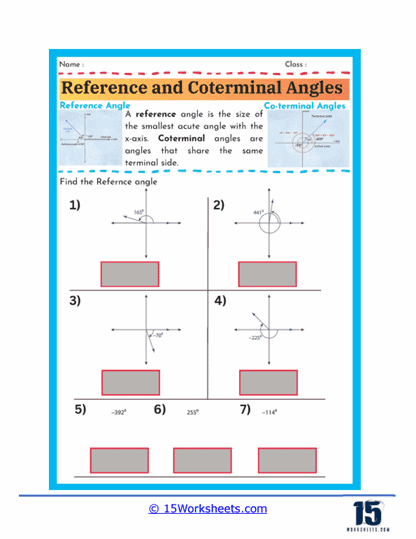
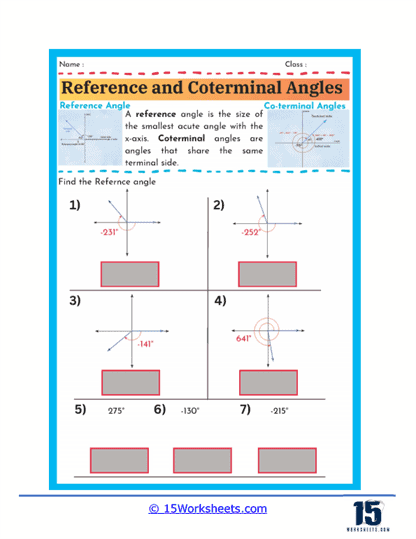
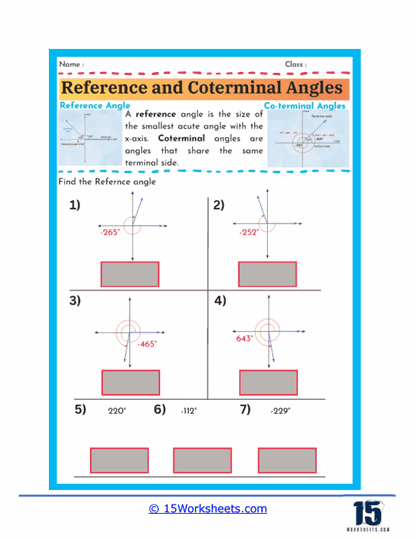
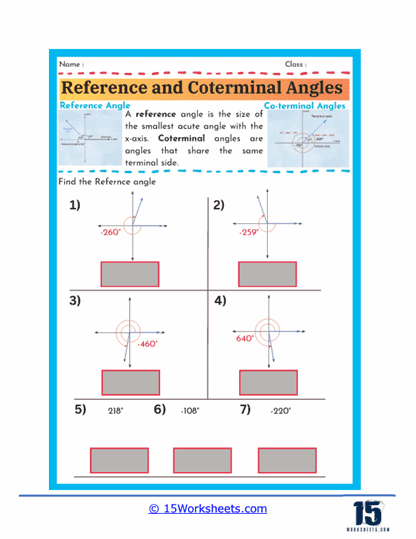
A reference angle is defined as the smallest angle that an angle makes with the x-axis, and it is always measured as a positive acute angle. It is important because it helps simplify the process of evaluating trigonometric functions for angles in any quadrant. When working with reference angles, students learn to visualize where the angle lies on the coordinate plane and then determine the acute angle that the given angle makes with the x-axis. This skill is particularly useful because the trigonometric functions of the reference angle are the same as those of the original angle, albeit with a possible change in sign depending on the quadrant.
Worksheets that focus on finding reference angles typically present students with a variety of angles, both positive and negative, and ask them to determine the corresponding reference angle. For example, a worksheet might provide angles such as 135°, -210°, or 300° and require students to find the reference angle for each. Through these exercises, students learn to apply the rules for finding reference angles, such as subtracting the angle from 180° or 360° when necessary or taking the absolute value for negative angles. These worksheets also help reinforce the concept that reference angles are always between 0° and 90°, regardless of the original angle’s position on the coordinate plane.
Coterminal angles are angles that share the same terminal side when drawn in standard position on the coordinate plane. They can be found by adding or subtracting full rotations, or 360° (or 2π2π radians), from a given angle. Coterminal angles are significant because they help students understand that an angle’s position is not unique; instead, it can represent multiple rotations or directions. This concept is particularly useful in periodic functions and in understanding the cyclical nature of trigonometric functions.
Worksheets that explore coterminal angles often present students with a given angle and ask them to find a positive and a negative coterminal angle. For instance, a worksheet might present an angle such as 45° and ask students to find the coterminal angles by adding and subtracting 360°. Similarly, for an angle given in radians, such as π/4, students would be required to add and subtract 2π2π to find the coterminal angles. These exercises help students practice the arithmetic involved in working with angles and rotations, reinforcing the understanding that coterminal angles differ by multiples of a full rotation.
Some worksheets combine both reference and coterminal angle concepts, presenting more complex problems that require students to first find a coterminal angle within a specific range, and then determine its reference angle. These combination problems challenge students to apply both concepts in a sequence, deepening their understanding of how angles relate to each other. For example, a problem might ask students to find the reference angle of -400°, which first requires finding a coterminal angle within the standard 0° to 360° range, and then determining the reference angle from that coterminal angle.
These combination problems are particularly useful in helping students see the connection between different trigonometric concepts. By working through these problems, students gain a more holistic understanding of how angles function on the unit circle and how different trigonometric operations can be applied in tandem. The process of solving these problems reinforces the cyclical nature of angles and prepares students for more advanced applications in trigonometry and calculus.
Another type of problem that often appears on reference and coterminal angles worksheets involves determining whether two given angles are coterminal. In these problems, students are given two angles and must determine if they share the same terminal side by evaluating whether their difference is a multiple of 360° (or 2π radians). This type of problem encourages students to engage in critical thinking, as they must apply their knowledge of coterminal angles in a more evaluative context rather than just calculating or identifying angles.
State and evaluate problems help students understand that coterminal angles are fundamentally about angle equivalency despite different rotations. This concept is essential in trigonometry, where periodicity and repeating cycles are core themes. By evaluating whether angles are coterminal, students learn to recognize patterns in angle measurement and apply these patterns to solve more complex problems in trigonometry and beyond.
While the primary goal of these worksheets is to build a strong foundation in trigonometric concepts, the skills learned are also highly applicable in real-world scenarios. For example, reference and coterminal angles are crucial in fields such as engineering, physics, and computer graphics, where precise angle measurements are often necessary. Understanding how to manipulate and work with angles, including identifying equivalent angles, is essential in designing systems, analyzing forces, and creating visual representations.
In computer graphics, for instance, angles are used to determine the orientation of objects and light sources. Understanding coterminal angles helps programmers and designers manage rotations and ensure that objects appear correctly from any perspective. Similarly, in physics, reference angles are often used to simplify the analysis of forces and motion, particularly when dealing with vectors and rotations. By mastering these concepts through worksheets, students are not only preparing for academic success but also equipping themselves with practical skills that are directly applicable to various technical fields.
Rounding and Precision in Angle Calculations
Many reference and coterminal angle worksheets also emphasize the importance of precision in trigonometric calculations. Problems that require students to round angles to the nearest degree or radian highlight the need for accuracy in mathematical computations. This focus on precision is particularly important as students progress to more advanced trigonometric applications, where small errors can lead to significant discrepancies in results.
These worksheets teach students to be meticulous in their calculations, reinforcing the idea that attention to detail is crucial in mathematics. Whether adding or subtracting full rotations or converting between degrees and radians, students learn to perform these operations with care, ensuring that their final answers are both accurate and reliable. This skill is essential not only in trigonometry but also in other areas of mathematics and science, where precision is paramount.
Through these exercises, students learn to visualize angles, perform accurate calculations, and apply their knowledge in both theoretical and practical contexts. The skills developed through working on these worksheets are essential for success in advanced trigonometry and calculus, as well as in real-world applications such as engineering, physics, and computer graphics. By mastering reference and coterminal angles, students lay the groundwork for a deeper understanding of trigonometry and its many applications.
What Are Reference and Coterminal Angles?
In trigonometry, reference angles and coterminal angles are fundamental concepts used to understand the relationships between angles and their trigonometric functions. A reference angle is the smallest angle that a given angle makes with the x-axis, always measured as a positive acute angle between 0° and 90° (or 0 and π/2 radians). It helps simplify the calculation of trigonometric functions by reducing any angle to an equivalent angle in the first quadrant, where trigonometric values are often easier to compute.
Coterminal angles, on the other hand, are angles that share the same initial and terminal sides when drawn in standard position on the coordinate plane. They can be found by adding or subtracting full rotations (360° or 2π radians) to a given angle. This property means that coterminal angles have identical sine, cosine, and tangent values, making them useful for solving trigonometric equations and simplifying expressions.
These concepts are crucial for understanding the periodic nature of trigonometric functions and are widely used in various mathematical and engineering applications. For instance, in fields such as physics and engineering, reference and coterminal angles are used to model wave patterns, oscillations, and rotations, where understanding the periodicity and symmetry of angles is essential. Additionally, in computer graphics, these angles help in calculating rotations and rendering objects accurately on a screen. By mastering reference and coterminal angles, students can develop a deeper understanding of trigonometry and its applications in real-world scenarios.