Scale Factors Worksheets
About These 15 Worksheets
These worksheets can help students understand the mathematical concept of scale factors, which involves enlarging or reducing shapes proportionally. These worksheets typically include a variety of exercises that focus on calculating, applying, and understanding how scale factors affect different geometric figures. Scale factor problems are critical in building a student’s understanding of geometry, proportions, and real-world applications like maps, blueprints, and models. Students learn how to determine how much a shape has been enlarged or reduced, and how the dimensions of one shape relate to another in terms of scale.
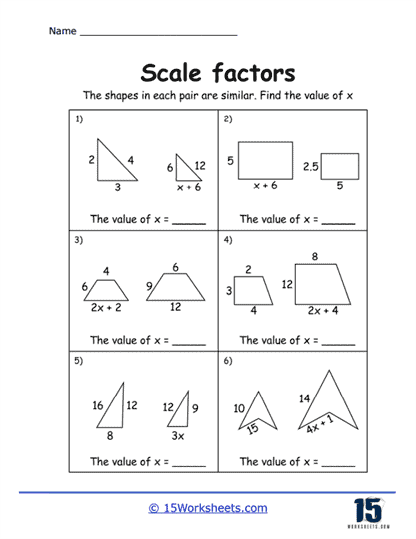
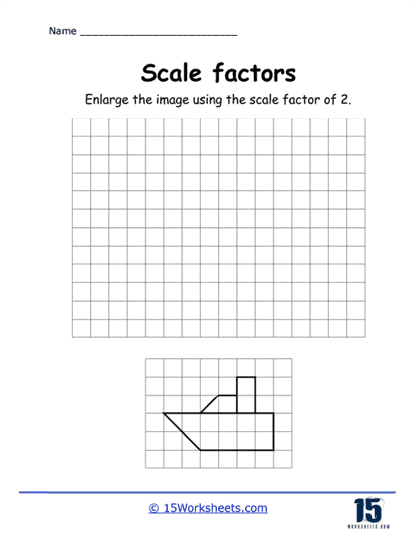
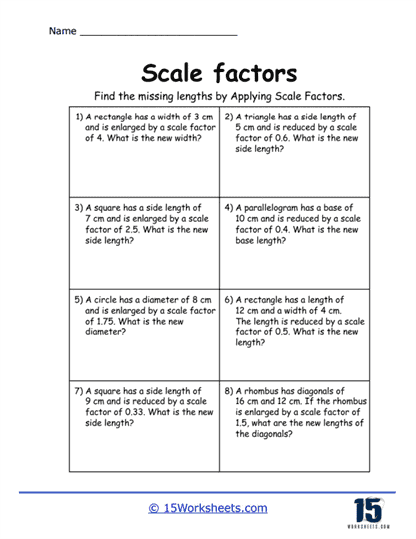
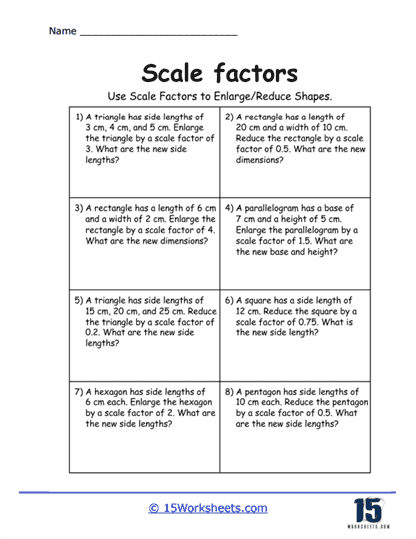
One of the primary types of problems you’ll find on these worksheets is basic calculations involving two similar shapes. These problems provide students with the dimensions of one shape and ask them to find the dimensions of a similar shape after applying a given scale factor. For example, if students are given a triangle with sides measuring 3 cm, 4 cm, and 5 cm, and are asked to apply a scale factor of 2, they would need to double each side to find the dimensions of the new triangle – 6 cm, 8 cm, and 10 cm. These problems help students grasp the basic concept of multiplying dimensions by a scale factor to either enlarge or reduce a figure.
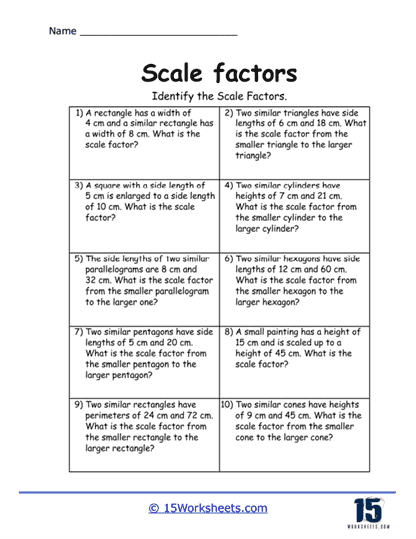
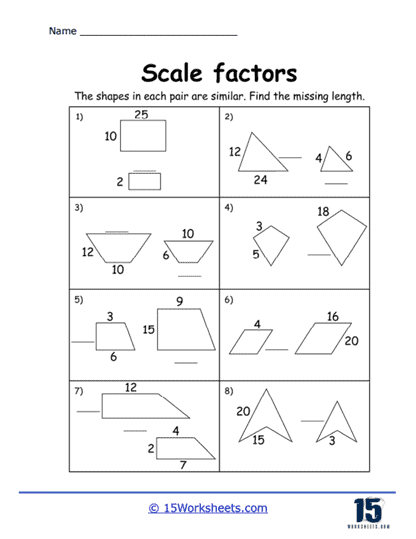
Another common type of problem involves reverse scale factor calculations, where students are given the dimensions of both the original and scaled shapes, and they must determine the scale factor used. For example, if a student is given a rectangle with dimensions of 6 cm by 8 cm and a similar rectangle with dimensions of 12 cm by 16 cm, they must determine the scale factor by dividing the dimensions of the larger rectangle by the corresponding dimensions of the smaller rectangle. In this case, the scale factor is 2. These types of problems teach students how to work backward, which reinforces their understanding of the proportional relationship between two shapes.
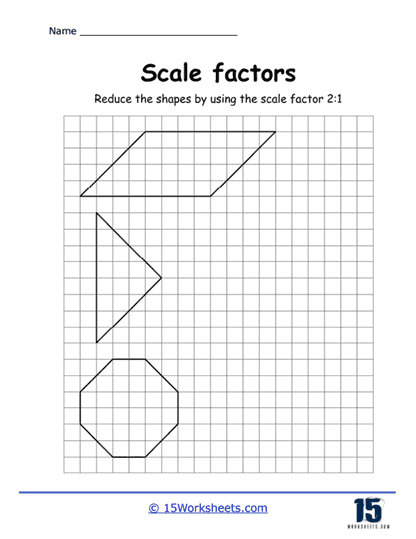
This collection of worksheets introduce the concept of using a scale factor to enlarge or reduce two-dimensional shapes such as squares, rectangles, triangles, and circles. Students practice applying scale factors to all the dimensions of these shapes, learning that each dimension must be multiplied by the same factor. This consistency across dimensions helps students recognize that scale factors maintain the proportions of the original shape, ensuring that the new shape is a true enlargement or reduction, not a distortion. For example, when applying a scale factor to a circle, students learn that both the radius and the diameter must be multiplied by the same factor, keeping the shape proportional.
Many worksheets also include problems where students must apply scale factors to more complex shapes or composite figures. Composite figures consist of multiple shapes combined together, such as a rectangle with a semicircle on top. When applying a scale factor to a composite figure, students must correctly scale each component of the shape. This requires them to pay close attention to detail and ensure that all dimensions of the figure, no matter how complex, are scaled proportionally. These types of problems help students develop precision in their calculations and strengthen their ability to visualize the effects of scale factors on more complicated shapes.
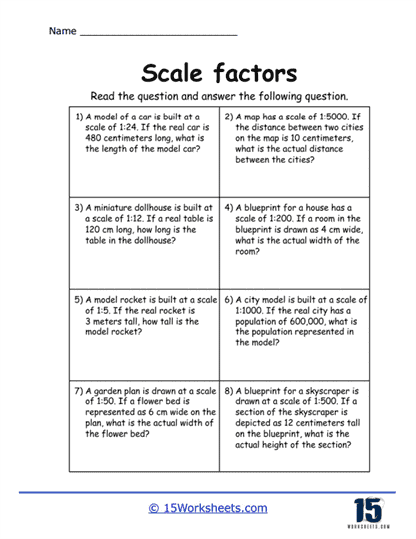
These worksheets include real-world applications, where students must apply their knowledge of scale factors to solve practical problems. For example, students might be given a floor plan of a house and asked to apply a scale factor to create a larger or smaller version of the plan. These problems often provide a scale, such as 1 inch representing 10 feet, and ask students to calculate the actual dimensions of rooms, doors, or windows based on the scale. By solving these problems, students learn how to apply the concept of scale factors beyond the classroom and understand its significance in fields like architecture, engineering, and art.
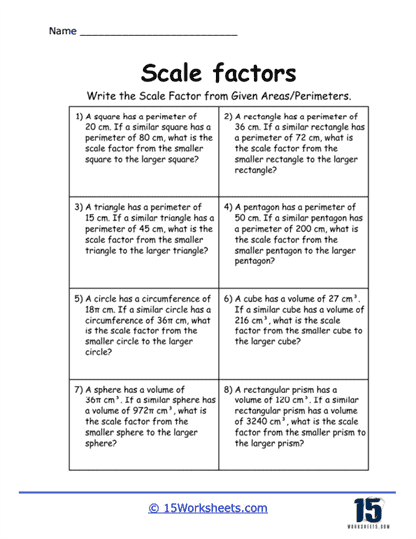
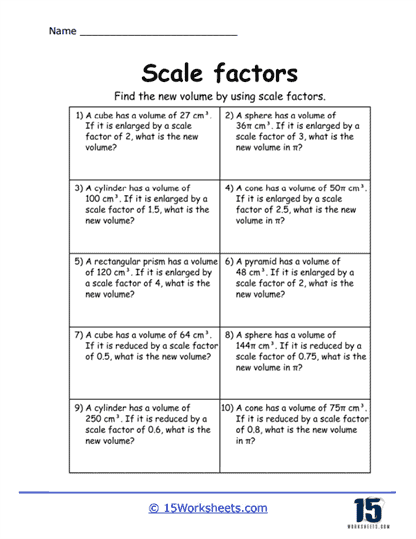
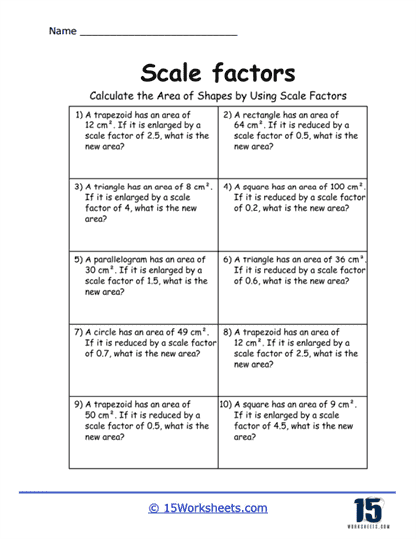
Another type of problem commonly found on these worksheets involves calculating areas and volumes of scaled shapes. When a shape is scaled by a certain factor, not only are the linear dimensions affected, but the area and volume are as well. Students are taught that when a shape is enlarged or reduced, the area is scaled by the square of the scale factor, while the volume is scaled by the cube of the scale factor. For instance, if a square is enlarged by a scale factor of 3, the area of the new square will be 9 times larger (since 3^2 = 9). Similarly, if a cube is enlarged by a scale factor of 2, the volume of the new cube will be 8 times larger (since 2^3 = 8). Understanding how scale factors affect area and volume is crucial for students as they explore more advanced mathematical concepts.
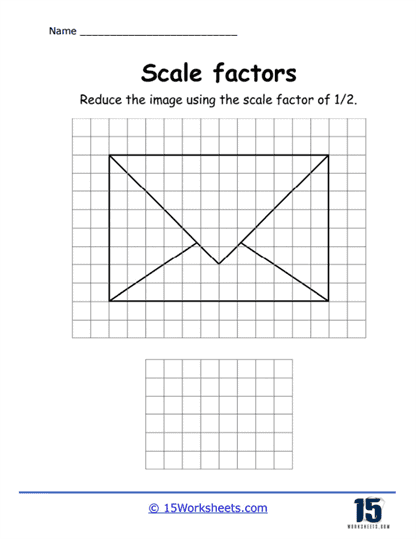
Some these worksheets also focus on the reverse process of reducing figures. Instead of enlarging shapes, students are asked to shrink them by applying a scale factor less than 1. For example, they might be given a rectangle with dimensions of 10 cm by 5 cm and asked to apply a scale factor of 0.5. In this case, they would need to multiply both dimensions by 0.5, resulting in a smaller rectangle with dimensions of 5 cm by 2.5 cm. These problems help students understand that scale factors can also reduce shapes and that the principles of proportionality apply in both directions. Learning how to work with scale factors less than 1 broadens their understanding of the concept and prepares them for more complex problem-solving scenarios.
In addition to the traditional exercises, this collection includes visual aids such as diagrams or grids. For example, a worksheet might show two similar shapes on a grid and ask students to calculate the scale factor by comparing the side lengths. Visual representations help students better understand the spatial relationships between the original and scaled shapes and provide a concrete way to visualize the effects of scaling. These types of problems also help students develop their spatial reasoning skills, which are essential for success in geometry and other STEM fields.
The worksheets often introduce multi-step problems that combine several skills. For example, a problem might ask students to first determine the scale factor between two similar shapes, then apply that scale factor to calculate the new dimensions of a scaled-up version of the shape, and finally find the area or volume of the enlarged shape. These problems help students connect different mathematical concepts and apply their knowledge in a more integrated way. Multi-step problems are great for reinforcing students’ understanding of scale factors while also encouraging them to think critically and logically through the steps needed to solve more complex problems.
What Are Scale Factors?
A scale factor is like a recipe for making something bigger or smaller while keeping its shape the same. Imagine you have a picture of a square, and you want to make a larger or smaller version of that square. The scale factor tells you how much to multiply each side of the square by. For example, if the scale factor is 2, you double the size of every side. If the scale factor is 0.5, you make each side half as long. It’s just a simple number that helps you change the size of something without changing its shape.
Scale factors play a crucial role in many real-world applications, particularly when we need to represent or work with objects or distances that are too large or too small to be easily managed at their actual size. Here are some key areas where scale factors are important:
Architecture and Construction
Architects and engineers regularly use scale factors when creating blueprints and models. These scaled-down representations allow them to:
– Design and visualize buildings before construction
– Communicate plans effectively to clients and construction teams
– Ensure proper proportions and measurements in the final structure
For example, an architect might use a scale of 1:100 for a building plan, meaning 1 cm on the drawing represents 100 cm (1 meter) in real life.
Cartography and Geography
Map-making relies heavily on scale factors to represent vast geographical areas on manageable-sized maps. This allows:
– Accurate representation of distances between locations
– Planning of routes and travel times
– Understanding of relative sizes of countries and continents
A road map, for instance, might use a scale where 1 inch represents 10 miles, allowing users to calculate real-world distances from the map.
Manufacturing and Engineering
Scale factors are crucial in:
– Creating prototypes and models of products
– Designing parts that need to fit together precisely
– Scaling up successful small-scale designs for mass production
Scientific Visualization
Scientists often use scale factors to:
– Represent microscopic structures like cells or atoms
– Model astronomical objects and distances
– Simulate large-scale phenomena like weather patterns or geological processes
Computer Graphics and Digital Imaging
Scale factors are important in:
– Resizing images without distortion
– Creating 3D models for animation and video games
– Zooming in and out of digital maps and designs
In all these applications, understanding and correctly applying scale factors is crucial for accuracy, efficiency, and effective communication of information. Whether it’s an architect designing a skyscraper, a cartographer mapping a continent, or a scientist modeling a molecule, scale factors allow us to work with and understand objects and systems that would otherwise be too large or small to manipulate directly.