Irrational Numbers Worksheets
About These 15 Worksheets
These worksheets are designed to help students navigate the complex landscape of irrational numbers, a fundamental component of the broader number system. By engaging with these worksheets, students learn not just to recognize irrational numbers, but also to appreciate their unique properties and how they differ from other number types, like integers and rational numbers. This enhanced understanding is pivotal as it lays the groundwork for more advanced mathematical concepts and ensures that students have a solid grasp of foundational principles.
These worksheets provide a variety of exercises that cater to different learning styles and objectives, from basic identification and approximation to more complex algebraic manipulations. These worksheets not only enhance students’ understanding of irrational numbers but also prepare them for advanced mathematical concepts, fostering a deeper appreciation and confidence in math.
Types of Exercises
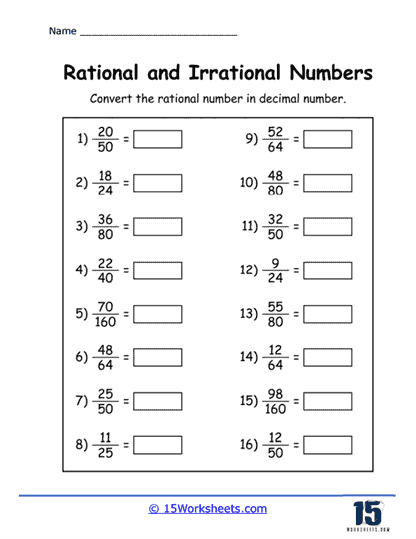
Identification Exercises – These exercises ask students to distinguish between rational and irrational numbers. Students are presented with a list of numbers and must identify which ones are irrational.
Approximation Exercises – Here, students practice approximating irrational numbers to a certain number of decimal places. This helps in understanding that these numbers have non-terminating, non-repeating decimals.
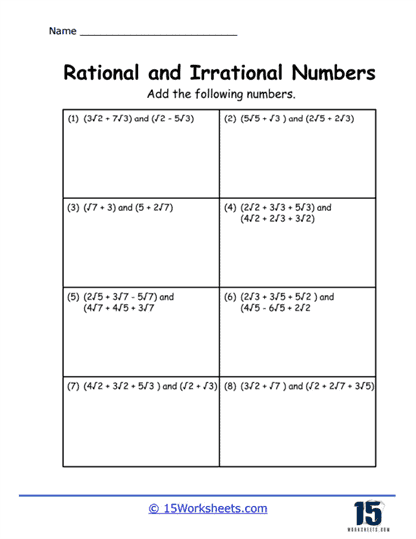
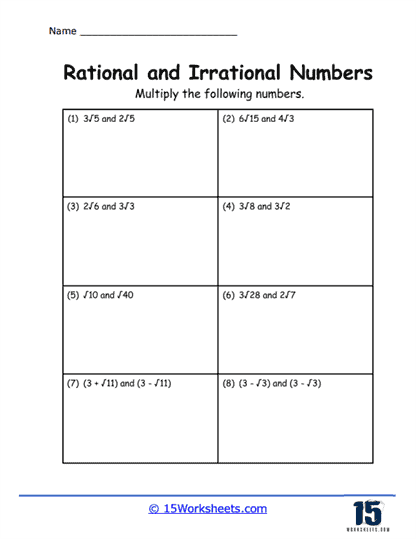
Operations with Irrational Numbers – These exercises involve performing arithmetic operations (addition, subtraction, multiplication, division) with irrational numbers, often combining them with rational numbers.
Graphical Representation – Students plot irrational numbers on a number line. This helps in visualizing the density of irrational numbers in the real number system.
Algebraic Manipulation – Advanced worksheets may include algebraic expressions involving irrational numbers, where students must simplify or solve equations.
Historical Context Questions – Some worksheets may include questions about the history and discovery of irrational numbers, to provide a broader understanding of the concept.
Comparison and Ordering – Exercises that require students to compare or order a set of irrational numbers, often alongside rational numbers.
The Benefits of These Worksheets
Development of Math Skills
Students’ engagement with irrational numbers worksheets leads to significant skill development. These skills include the ability to approximate irrational numbers, a deeper sense of number theory, and proficiency in performing various operations with different types of numbers. The practice of rounding off irrational numbers to a certain number of decimal places, for instance, is not just a mathematical procedure but also a critical thinking exercise. It requires students to understand the nature of non-terminating, non-repeating decimals and their representation in real-world contexts. Such exercises enhance students’ numerical dexterity and lay a robust foundation for more sophisticated mathematical tasks.
A solid understanding of irrational numbers is a cornerstone for success in higher-level mathematics, including disciplines such as algebra, trigonometry, and calculus. Worksheets focusing on irrational numbers serve as an essential foundation for these advanced studies. They ensure that students are not only familiar with these numbers but also comfortable in manipulating and utilizing them in various mathematical contexts. This preparedness is critical for academic progression and success in more challenging mathematical courses.
Enhancement of Problem-Solving and Critical Thinking
Irrational numbers worksheets are instrumental in bolstering students’ problem-solving and critical thinking skills. When students work with irrational numbers, they are often required to apply multiple steps and adopt various strategies to reach solutions. This process fosters an environment where analytical thinking, logic, and creativity are paramount. By tackling problems that involve irrational numbers, students learn to navigate through complex scenarios, an ability that is invaluable not just in mathematics but in real-life situations as well.
Real-World Applications
Irrational numbers worksheets often include word problems and scenarios that apply these numbers in real-life contexts. This approach demonstrates the practicality and relevance of irrational numbers, showing students how these abstract concepts are used in everyday life. Whether it’s in measuring distances, understanding scientific phenomena, or dealing with finances, the application of irrational numbers is vast. By encountering these practical applications, students can better appreciate the significance of what they are learning and how it relates to the world outside the classroom.
Building Confidence
Mastering a challenging topic like irrational numbers can significantly boost a student’s confidence in their mathematical abilities. As they progress through the worksheets and begin to understand and solve problems involving irrational numbers, they gain a sense of achievement and empowerment. This confidence is not only important for their current mathematical endeavors but also fosters a positive attitude towards future mathematical challenges.
What are Irrational Numbers?
Irrational numbers are a category of real numbers that cannot be expressed as a simple fraction or ratio of two integers. Their most defining characteristic is that their decimal expansions are non-terminating and non-repeating. This means that these numbers go on infinitely without displaying a repeating pattern. Understanding the properties and examples of irrational numbers is crucial for grasping more complex mathematical concepts.
A number is considered irrational if it cannot be expressed as a fraction of two integers (i.e., it cannot be written in the form a/b, where “a” and “b” are integers and “b” is not equal to zero). In other words, an irrational number cannot be represented as a simple ratio of two whole numbers.
Properties of Irrational Numbers
Non-terminating and Non-repeating Decimals – An irrational number cannot be written as a terminating decimal (one that ends) or as a repeating decimal (one where digits or groups of digits repeat endlessly).
Cannot be Expressed as a Fraction – Unlike rational numbers, which can be written as the quotient of two integers (like ½ or -3/4), irrational numbers cannot be expressed in this form.
Density on the Number Line – Between any two rational numbers, there are infinitely many irrational numbers. This means they are densely packed on the number line, filling the gaps between rational numbers.
Unique Decimal Expansion – Each irrational number has a unique decimal expansion, which helps in distinguishing one irrational number from another.
Closed Under Certain Operations – The set of irrational numbers is not closed under operations like addition, subtraction, multiplication, and division. This means combining two irrational numbers with these operations can sometimes result in a rational number. For example, the sum of certain irrational numbers can be a rational number.
It’s important to note that not all irrational numbers have simple algebraic expressions or easily recognizable patterns. Many irrational numbers are defined through mathematical analysis and are characterized by their non-repeating, non-terminating decimal expansions and their inability to be expressed as fractions of integers.
Examples of Irrational Numbers and Their Uses
The Square Root of 2 (√2)
Property – This number is the length of the diagonal of a square with sides of one unit.
Use in Geometry – It’s frequently used in calculations involving right-angled triangles and other geometric shapes.
Example: If you have a square with side lengths of 1 unit, the diagonal’s length is √2 units. This is derived using the Pythagorean theorem.
Pi (Π)
Property – Approximately 3.14159, Π represents the ratio of a circle’s circumference to its diameter.
Use in Calculations Involving Circles – It’s used in a wide range of mathematical and scientific fields, including geometry, trigonometry, and physics.
Example: To find the circumference of a circle with a diameter of 5 units, multiply the diameter by Π (5 x Π ≈ 15.708 units).
Euler’s Number (e)
Property – Approximately 2.71828, e is the base of natural logarithms and is deeply embedded in the fabric of calculus and complex analysis.
Use in Exponential Growth and Decay Models – It appears in various areas of science, especially in growth and decay problems.
Example: In finance, the formula for continuously compounded interest uses e. If you have $1000 in a bank account that offers a 5% annual interest rate compounded continuously, the formula to calculate the amount after t years is 1000 x e0.05t.
These examples highlight how irrational numbers are not just theoretical concepts but have practical applications in various fields, from geometry and finance to physics and engineering. Their unique properties make them an integral part of the mathematical world, enabling accurate descriptions and predictions of natural phenomena and human-made structures.