Properties of Real Numbers Worksheets
About These 15 Worksheets
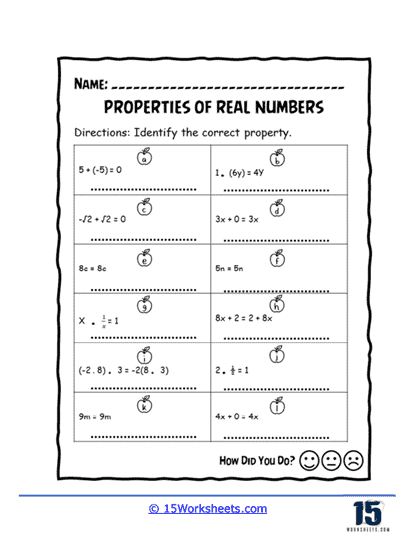
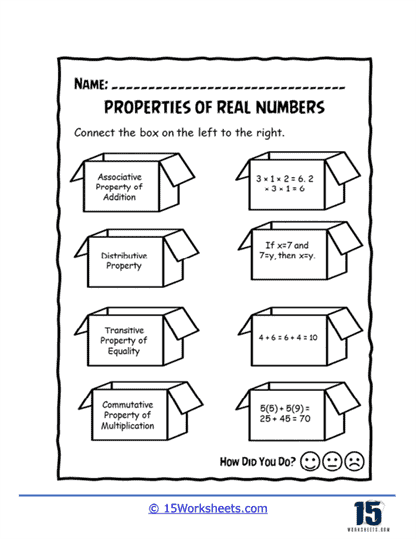
These worksheets help students learn and apply the fundamental characteristics and rules associated with real numbers. They focus on the properties that govern the operations of addition, subtraction, multiplication, and division of real numbers.
These worksheets include a variety of problems that require students to apply these properties to simplify expressions, solve equations, and perform operations. By working through these worksheets, students gain a deeper understanding of the foundational rules that govern arithmetic with real numbers.
Understanding the properties of real numbers is pivotal in mathematics because they form the foundation upon which more complex mathematical concepts and techniques are built. These properties provide a consistent framework that allows mathematicians and students alike to manipulate and work with numbers in predictable ways. For example, when solving algebraic equations, knowing how numbers interact with one another-whether they’re being added, multiplied, or distributed-helps in simplifying and solving for unknown variables.
These properties aren’t just arbitrary rules; they reflect the inherent nature of numbers and arithmetic, and by understanding them, one gains a deeper insight into the logic and structure of mathematics. This understanding fosters confidence and efficiency, whether one is performing basic arithmetic or delving into more intricate mathematical problems. In essence, the properties of real numbers serve as both a guide and a tool, streamlining computations and providing a solid basis for mathematical reasoning.
The Fundamental Properties of Real Numbers
1. Commutative Property
a) Commutative Property of Addition
Example Displayed With Variables – a + b = b + a
Explanation: When two numbers are added, the sum is the same regardless of the order of the addends.
Example Displayed With Real Numbers – 7 + 5 = 5 + 7
b) Commutative Property of Multiplication
Example Displayed With Variables – a × b = b × a
Explanation: When two numbers are multiplied, the product is the same regardless of the order of the multipliers.
Example Displayed With Real Numbers – 7 × 5 = 5 × 7
2. Associative Property
a) Associative Property of Addition
Example Displayed With Variables – (a + b) + c = a + (b + c)
Explanation: The way in which numbers are grouped when they are added does not affect the sum.
Example Displayed With Real Numbers – (3 + 4) + 5 = 3 + (4 + 5)
b) Associative Property of Multiplication
Example Displayed With Variables – (a × b) × c = a × (b × c)
Explanation: The way in which numbers are grouped when they are multiplied does not affect the product.
Example Displayed With Real Numbers – (3 × 4) × 5 = 3 × (4 × 5)
3. Distributive Property
Example Displayed With Variables – a × (b + c) = a × b + a × c
Explanation: Multiplying a number by the sum of two other numbers is the same as multiplying the number by each of the two numbers and then adding the products together.
Example Displayed With Real Numbers – 5 × (3 + 4) = 5 × 3 + 5 × 4
4. Identity Property
a) Identity Property of Addition
Example Displayed With Variables – a + 0 = a
Explanation: Any number plus zero equals the original number.
Example Displayed With Real Numbers – 7 + 0 = 7
b) Identity Property of Multiplication
Example Displayed With Variables – a × 1 = a
Explanation: Any number multiplied by one equals the original number.
Example Displayed With Real Numbers – 7 × 1 = 7
5. Inverse Property
a) Additive Inverse
Example Displayed With Variables – a + (-a) = 0
Explanation: For every real number, there exists another number such that their sum is zero.
Example Displayed With Real Numbers – 5 + (-5) = 0
b) Multiplicative Inverse
Example Displayed With Variables – a x 1/a = 1 (where a is not equal to 0)
Explanation: For every non-zero real number, there exists another number such that their product is one.
Example Displayed With Real Numbers – 5 x 1/5 = 1
6. Property of Zero (Multiplication)
Example Displayed With Variables – a × 0 = 0
Explanation: Any real number multiplied by zero is zero.
Example Displayed With Real Numbers – 5 × 0 = 0