Consecutive Numbers Worksheets
About These 15 Worksheets
These worksheets will help students understand and work with sequences of numbers that follow one another in order, without gaps. These numbers, such as 1, 2, 3, or 10, 11, 12, are called “consecutive” because each number is one unit greater than the previous one. Consecutive Numbers worksheets provide a variety of exercises to strengthen students’ understanding of number patterns, number sense, and arithmetic operations. By focusing on consecutive numbers, these worksheets help students build a foundational understanding of how numbers relate to one another in sequence, which is crucial for mastering higher-level math concepts.
Identifying Consecutive Numbers
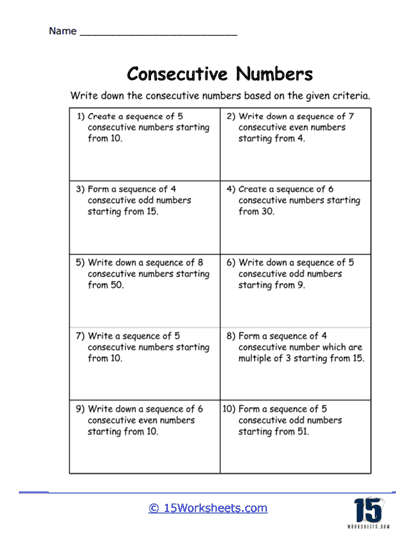
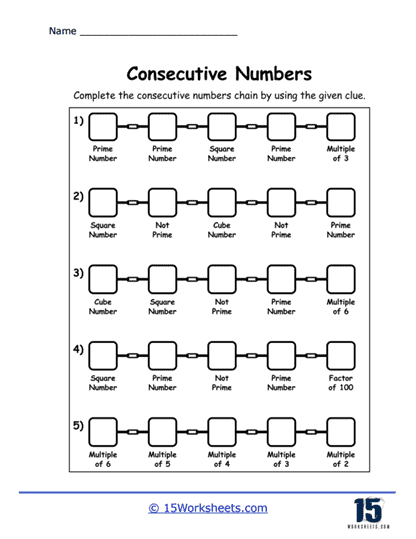
One of the most common types of exercises you’ll find on these worksheets is the task of identifying consecutive numbers. In this type of problem, students are given a sequence of numbers, and they must determine which numbers follow one another in a consecutive order. For instance, a worksheet might present the numbers 4, 5, 6, 8, 9, and ask students to circle the consecutive numbers in the set. The goal here is to reinforce the idea that consecutive numbers follow one another without skipping any values.
Identifying consecutive numbers teaches students number sequencing, which is a foundational math skill. It helps students recognize patterns and improves their ability to mentally navigate the number line. By working through these types of problems, students develop their number sense and become more comfortable with identifying the relationships between numbers. This kind of exercise can also be adapted for different difficulty levels by using larger numbers or even negative numbers, which introduces students to the concept of consecutive integers that can extend below zero.
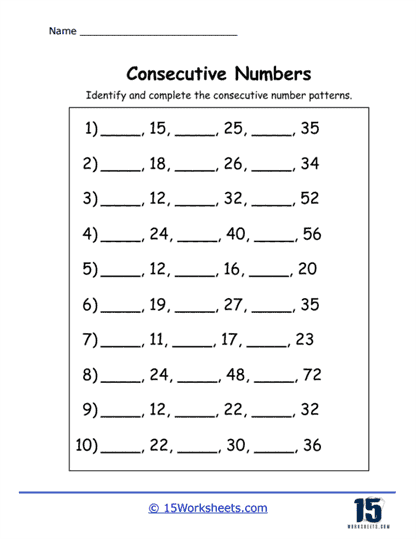
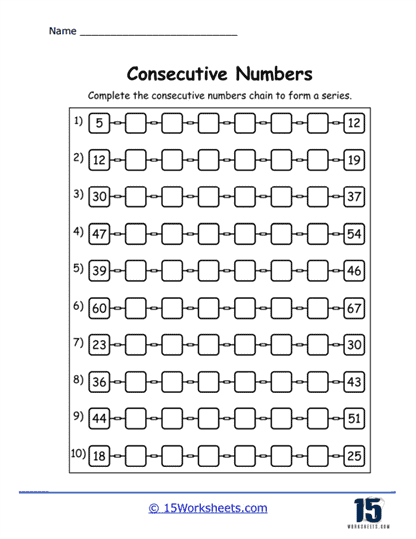
Filling in Missing Numbers
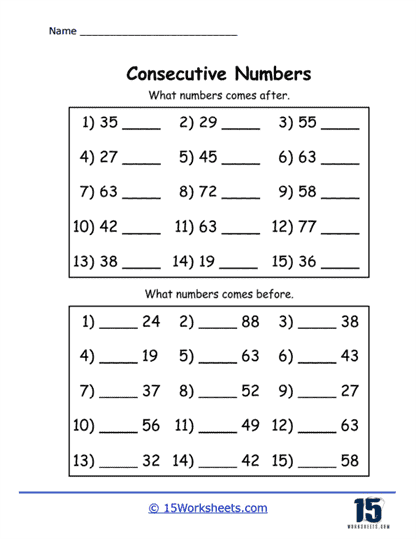
Another common exercise on this collection of worksheets is filling in the missing numbers in a sequence. For example, a worksheet might provide a sequence like 2, __, 4, __, 6, and ask students to fill in the blanks. This type of exercise reinforces the understanding that consecutive numbers are evenly spaced and differ by exactly one unit. It also helps students practice counting, as they must determine what number logically comes next in the sequence.
Filling in missing numbers builds on the concept of identifying consecutive numbers, but it takes the skill to the next level by requiring students to actively recall and apply their knowledge. This helps students solidify their understanding of counting in both forward and backward directions. Additionally, this type of task can be adjusted to introduce more advanced concepts, such as filling in the blanks with negative numbers or working with larger numbers. Teachers might also use these worksheets to introduce consecutive even or odd numbers, which helps students explore patterns within different sets of numbers.
Adding and Subtracting
Once students understand how to identify and fill in consecutive numbers, worksheets may introduce problems that involve adding or subtracting consecutive numbers. For instance, a problem might ask students to find the sum of the first five consecutive numbers, such as 1 + 2 + 3 + 4 + 5. Alternatively, students may be asked to subtract consecutive numbers, such as 10 – 9 – 8 – 7.
These types of problems help students build fluency with basic arithmetic operations, like addition and subtraction, and teach them how to recognize patterns in sums and differences. For example, adding consecutive numbers often results in a recognizable pattern, which can help students anticipate the results and develop mental math strategies. Subtraction problems that involve consecutive numbers are similarly useful because they help students practice counting backward and reinforce the concept of order and magnitude.
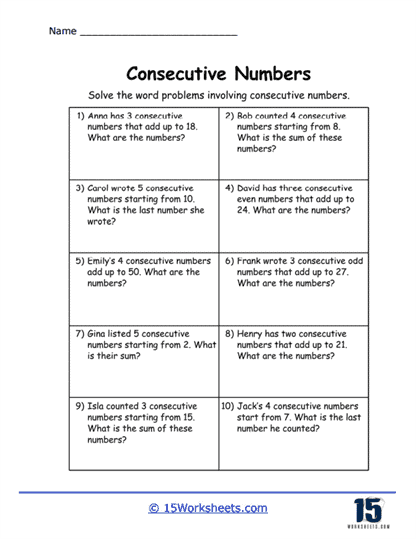
Solving Word Problems
Word problems that involve consecutive numbers encourage critical thinking and problem-solving skills. They help students see the practical applications of math and understand how consecutive numbers can be used to model real-world situations. These problems also build algebraic thinking by introducing students to the idea of using variables to represent unknown numbers. As students become more comfortable with these concepts, they can begin solving more complex problems involving larger sets of consecutive numbers or using other operations, such as multiplication or division.
Exploring Even and Odd Consecutive Numbers
Working with even and odd consecutive numbers teaches students about number properties and how certain types of numbers behave in sequences. This type of exercise also helps reinforce students’ understanding of the difference between even and odd numbers, as well as the arithmetic patterns associated with them. For instance, students might notice that adding two odd consecutive numbers always results in an even number. Recognizing these types of patterns helps students develop a deeper understanding of number theory and sets the stage for more advanced mathematical concepts.
Finding the Average
Another valuable exercise found on these worksheets is finding the average of a set of consecutive numbers. For example, a problem might ask students to calculate the average of the numbers 3, 4, and 5. In this case, students would add the numbers together and divide by 3 to find the average. This type of problem not only reinforces basic arithmetic operations but also introduces the concept of averages, which is a key statistical skill.
Finding the average of consecutive numbers teaches students how to work with sets of data and introduces them to the idea of central tendency. It also helps students recognize patterns in consecutive numbers, such as the fact that the average of any set of consecutive numbers will always be the middle number. This insight can help students develop mental math strategies for quickly finding averages without needing to perform every calculation.
Investigating Patterns in Sums
You will find problems that encourage students to investigate patterns in the sums of consecutive numbers. For example, students might be asked to find the sum of the first n consecutive numbers, such as 1 + 2 + 3 + … + 10. Through these types of problems, students can explore mathematical patterns, such as the fact that the sum of the first n consecutive numbers can be found using the formula n(n + 1) / 2.
Investigating patterns in sums helps students develop a deeper understanding of how numbers work together in sequences. These types of problems encourage algebraic thinking and pattern recognition, which are important skills for higher-level mathematics. By exploring these patterns, students also begin to see the connections between different areas of math, such as arithmetic, algebra, and geometry.
Exploring Differences
In addition to sums, some Consecutive Numbers worksheets ask students to explore the differences between consecutive numbers. For instance, a problem might ask students to subtract each number in a sequence from the next number and observe the pattern in the differences. This type of problem helps students recognize that the difference between any two consecutive numbers is always 1.
Exploring differences between consecutive numbers teaches students about number patterns and relationships. It also reinforces the concept of distance on the number line and helps students develop a better understanding of subtraction. By working through these types of problems, students become more comfortable with number sequences and gain a stronger sense of how numbers relate to one another in a mathematical context.
Introducing Algebraic Expressions
As students become more advanced, these worksheets can help introduce algebraic expressions that involve consecutive numbers. For example, a problem might ask students to find three consecutive numbers whose product is 24. To solve this problem, students must set up and solve an equation using variables, such as x(x + 1)(x + 2) = 24.
These types of problems introduce students to algebraic thinking and help them develop their skills in setting up and solving equations. They also provide an opportunity for students to practice working with variables and expressions in a meaningful context. By exploring algebraic expressions with consecutive numbers, students can begin to see how different areas of math are connected and how algebra can be used to solve real-world problems.