Parallelogram and Rhombus Worksheets
About Our Perimeter of Parallelograms and Rhombus Worksheets
These worksheets introduce students to the concept of perimeter by providing step-by-step exercises that guide them through calculating the total distance around each shape. Through these structured activities, learners become more familiar with the properties of parallelograms and rhombuses, such as equal opposite sides and congruent angles, reinforcing their grasp of key geometric principles. Whether working with given side lengths or solving problems that require applying algebraic expressions, students gain hands-on experience in determining perimeters, making abstract mathematical concepts more concrete and accessible.
Beyond just learning formulas, these worksheets help students sharpen their problem-solving and critical-thinking skills. By working through various scenarios, such as finding missing side lengths or solving real-world perimeter problems, students improve their ability to analyze and apply mathematical concepts in practical situations. Additionally, these exercises enhance measurement skills, preparing students for more advanced geometry and real-life applications, such as construction, design, and engineering. Overall, perimeter worksheets for parallelograms and rhombuses provide an interactive and engaging way for students to build confidence in geometry while reinforcing fundamental math skills that will benefit them in future academic and professional endeavors.
Mathematical Skills Explored
Geometry and Spatial Reasoning
Students develop their ability to visualize and analyze the distinct properties of parallelograms and rhombuses, reinforcing their understanding of geometric principles. By working through exercises that require them to recognize characteristics such as equal opposite sides, parallel lines, and congruent angles, they become adept at differentiating these shapes from other quadrilaterals. Additionally, they explore how these properties influence real-world applications, such as in architecture and design, where accurate shape identification is crucial. Through hands-on activities like drawing, labeling, and comparing figures, students refine their spatial reasoning skills, which are essential for understanding advanced geometric concepts. This foundational knowledge not only helps in academic settings but also enhances critical thinking and problem-solving skills in practical situations outside the classroom.
Measurement
These worksheets challenge students to accurately measure the sides of parallelograms and rhombuses using standard measurement tools, reinforcing their ability to work with different units. They gain practical experience using rulers, measuring tapes, and digital tools to record lengths in units such as centimeters, meters, inches, and feet. Additionally, students practice converting between different measurement units, which strengthens their ability to work within both the metric and imperial systems, an essential skill for various scientific and engineering applications. By engaging in measurement-based activities, they develop precision and attention to detail, skills that are valuable in disciplines such as physics, engineering, and technical trades. Mastering these measurement techniques not only helps students in geometry but also prepares them for real-world tasks that require accurate calculations, such as construction and design projects.
Algebraic Manipulation
Calculating the perimeter of parallelograms and rhombuses requires students to apply algebraic formulas, reinforcing their ability to manipulate mathematical expressions. They practice substituting given values into formulas like P = 2(a + b) for parallelograms and P = 4s for rhombuses, ensuring they understand the role of each variable in the calculation. Additionally, they encounter problems where they must rearrange equations to solve for unknown side lengths, helping them build fluency in working with algebraic expressions. These exercises not only strengthen their arithmetic skills but also prepare them for more advanced topics in algebra, such as solving for variables and working with equations in different contexts. By integrating algebra into geometry, students see the interconnectedness of mathematical disciplines, which enhances their overall problem-solving abilities.
Problem-Solving
Through these worksheets, students enhance their ability to systematically approach and solve perimeter-related problems with logical reasoning. They learn to break down each problem by identifying known values, determining which formula to apply, and performing calculations step by step. As they work through word problems and complex scenarios, they develop persistence and analytical thinking, which are essential skills for tackling higher-level mathematics. Additionally, they encounter real-life applications, such as calculating fencing requirements for a garden or determining the border length of a picture frame, making their learning experience more practical and engaging. By mastering problem-solving techniques through perimeter exercises, students build the confidence needed to tackle more advanced mathematical challenges in future coursework and everyday decision-making.
Types of Exercises and Practice Problems
The worksheets on the perimeter of parallelograms and rhombuses typically include a variety of exercises and practice problems, such as:
Identification and Calculation – Students begin by identifying key components of parallelograms and rhombuses, such as their sides and angles. They label these dimensions, which is an essential step in preparing for perimeter calculations. Recognizing the properties of these shapes, including the equal lengths of opposite sides in parallelograms and the congruent sides in rhombuses, helps build a strong geometric foundation. By thoroughly understanding these characteristics, students can confidently analyze and differentiate between these quadrilaterals.
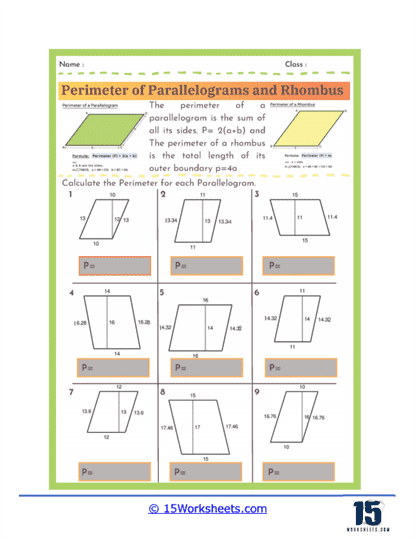
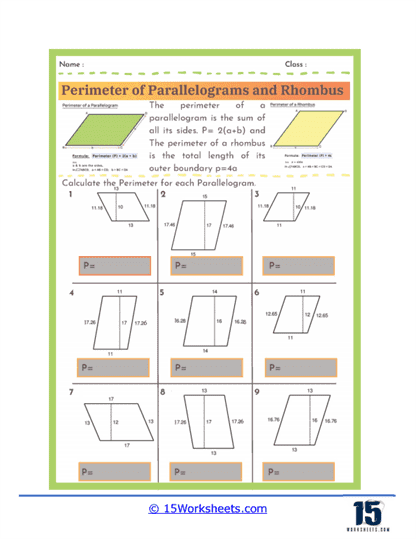
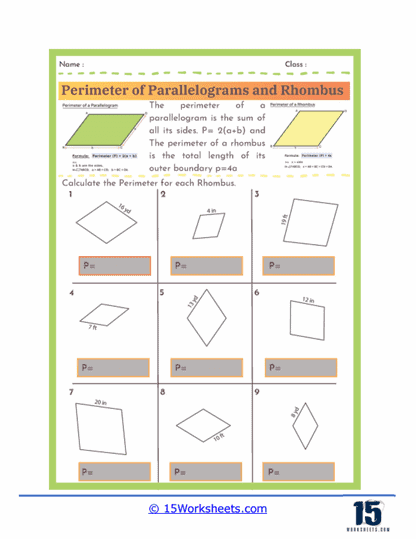
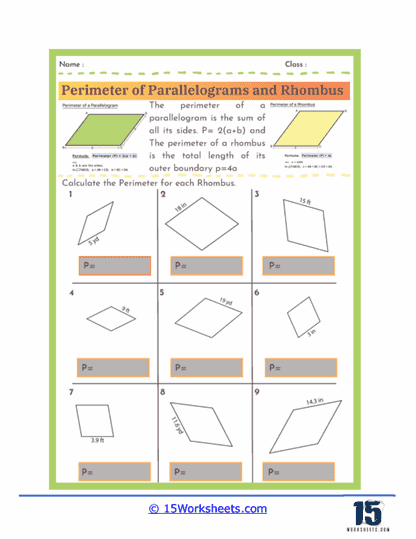
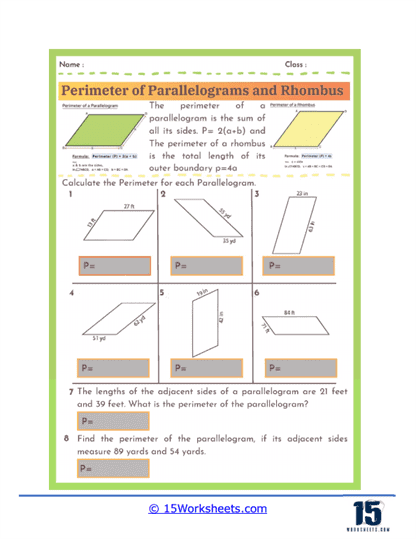
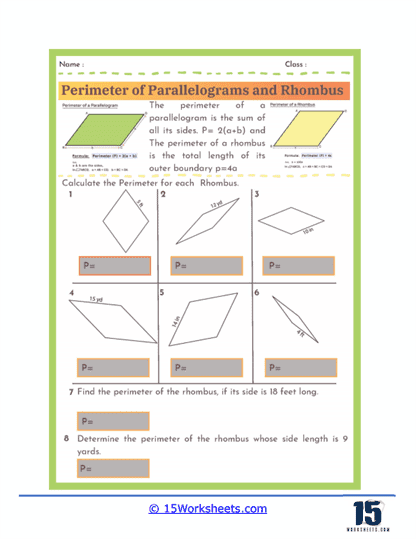
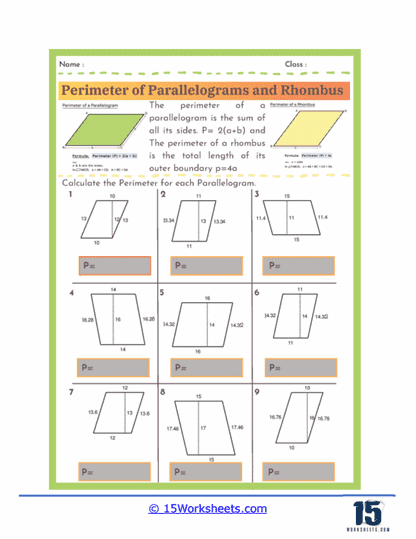
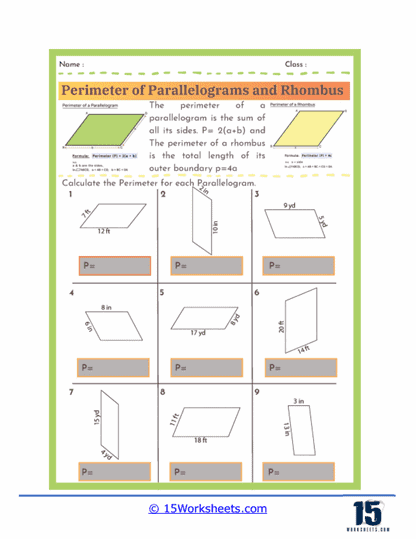
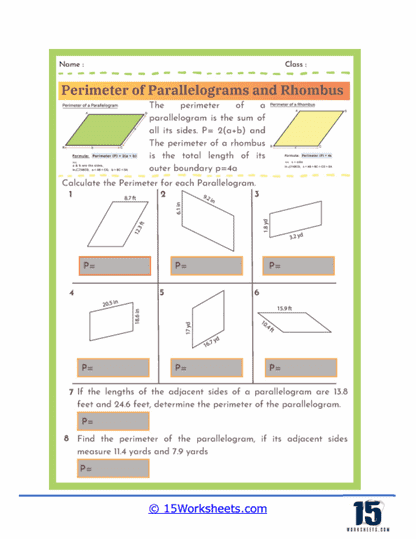
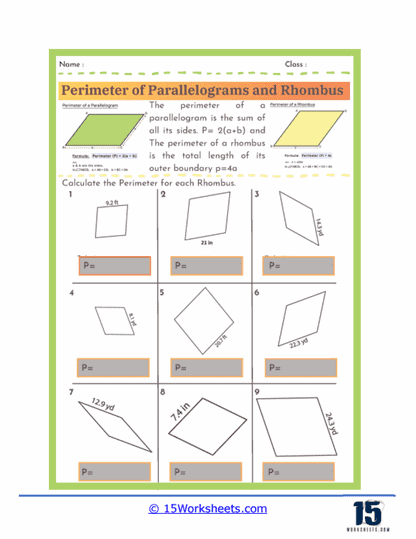
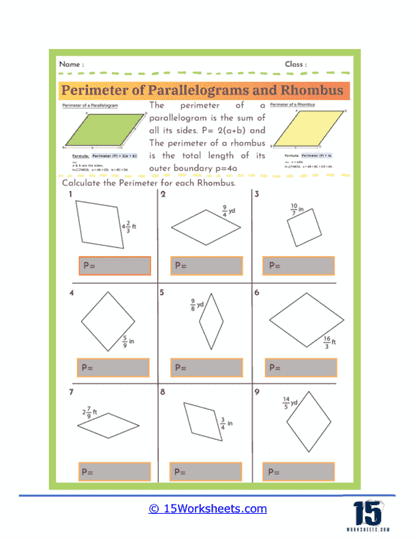
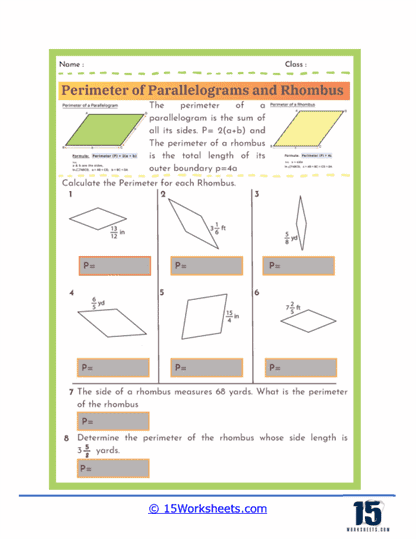
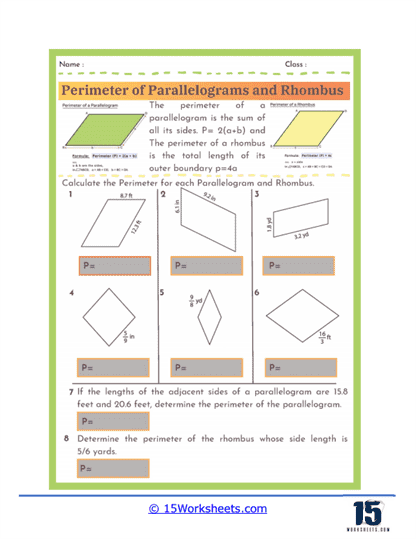
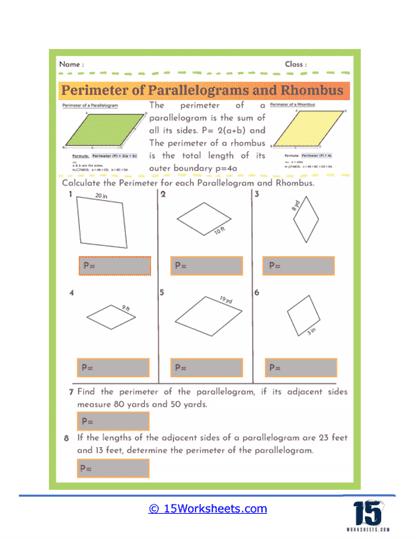
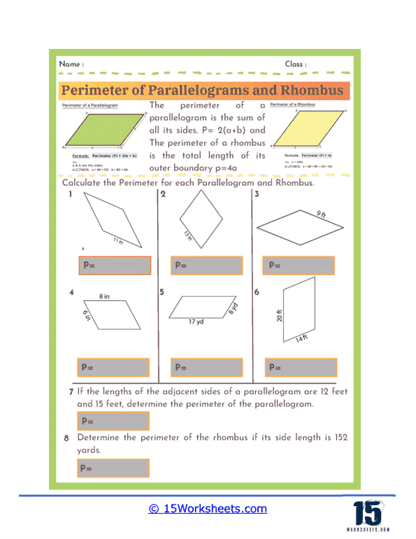
Perimeter Formulas – The worksheets introduce students to the standard formulas used to calculate the perimeter of parallelograms and rhombuses. For a parallelogram, the perimeter is given by the formula P = 2(a + b), where a and b represent the lengths of the opposite sides. For a rhombus, since all four sides are equal, the perimeter is simply P = 4a, where a is the length of one side. Understanding these formulas allows students to quickly determine perimeters without needing to measure every individual side.
Worked Examples – Each worksheet includes worked examples that demonstrate the application of perimeter formulas in solving specific problems. These examples provide a step-by-step breakdown of how to substitute given values and perform necessary calculations. By following these detailed explanations, students gain confidence in using mathematical formulas accurately. Reviewing multiple examples also helps reinforce different problem-solving approaches, ensuring that students understand the concept from various perspectives.
Practice Problems – The core of these worksheets consists of practice problems that allow students to apply their understanding. These exercises vary in complexity, ranging from straightforward perimeter calculations to multi-step problems that require additional reasoning. Some problems may involve comparing the perimeters of different shapes, while others challenge students to determine missing side lengths when given the total perimeter. This variety ensures that students of all skill levels can develop and strengthen their problem-solving abilities.
Real-World Applications – Many worksheets incorporate real-life scenarios where students must use perimeter calculations in practical situations. These problems might involve determining the fencing needed for a garden shaped like a parallelogram or calculating the border length of a diamond-shaped sign. Applying perimeter concepts to real-world contexts helps students see the relevance of mathematics beyond the classroom. By solving these application-based problems, students develop a deeper appreciation for how geometry is used in everyday life.
Benefits of These Worksheets
Enhanced Understanding of Geometry – These worksheets provide a structured approach to learning geometry, ensuring students grasp the essential properties of parallelograms and rhombuses. Through guided exercises, students can visualize how these shapes function within geometric principles. Step-by-step problem-solving helps reinforce key concepts such as angles, diagonals, and congruency. By mastering these foundations, students develop a deeper appreciation for geometry and its logical structure.
Improved Mathematical Skills – Working through these worksheets strengthens students’ ability to measure, analyze, and manipulate geometric figures with accuracy. They develop essential algebraic and problem-solving skills that are critical for advanced math courses. The exercises promote logical thinking, helping students break down complex problems into manageable steps. Mastering these skills enhances overall mathematical fluency, preparing students for future academic success.
Practical Applications – Students engage with real-world scenarios where geometry plays a crucial role, reinforcing the subject’s importance beyond the classroom. By solving problems related to fields like architecture, engineering, and design, they see how these concepts are applied in various careers. The worksheets help bridge the gap between theoretical knowledge and practical use, making math more engaging and relevant. Understanding these applications fosters a greater interest in STEM-related subjects and professions.
Increased Confidence – Consistent practice with these worksheets allows students to build a strong mathematical foundation, reducing anxiety toward complex problems. As they successfully complete exercises, their confidence in tackling geometry-related questions improves. The structured nature of the worksheets provides a sense of achievement, motivating students to take on more advanced challenges. Developing this self-assurance fosters a positive attitude toward learning math and problem-solving in general.
Example Problem
Find the perimeter of a parallelogram where one side measures 13.8 feet and the adjacent side measures 24.6 feet.
Step-by-Step Solution:
1. Identify the sides:
a. One side of the parallelogram is 13.8 feet.
b. The adjacent side is 24.6 feet.
2. Recall the formula for the perimeter of a parallelogram:
Perimeter = 2(a + b) where a and b are the lengths of the adjacent sides.
3. Substitute the given side lengths into the formula:
a = 13.8 feet
b = 24.6 feet
4. Calculate the sum of the sides:
a + b = 13.8 + 24.6 = 38.4 feet
5. Multiply the sum by 2 to find the perimeter:
Perimeter = 2 x 38.4 = 76.8 feet
6. Answer: The perimeter of the parallelogram is 76.8 feet