Squares and Rectangles Worksheets
About Perimeter of Squares and Rectangles Worksheets
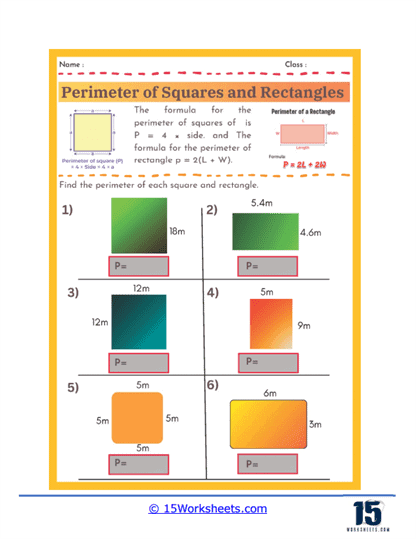
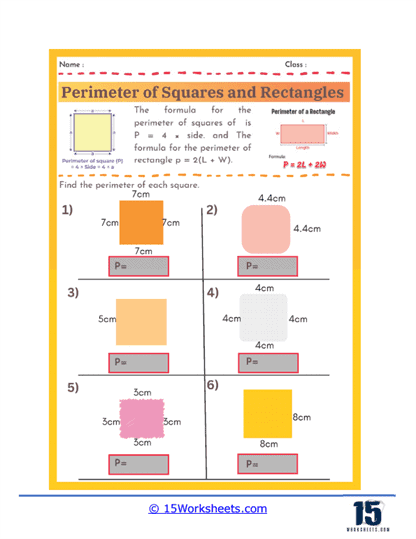
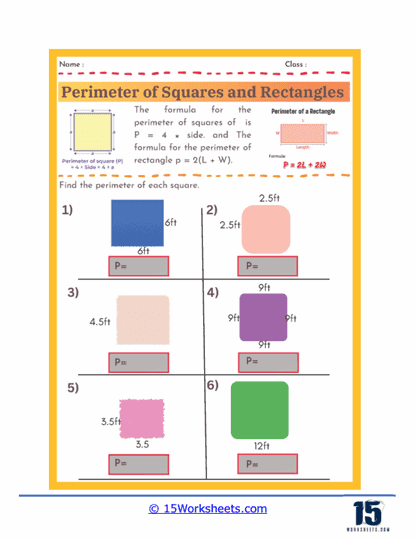
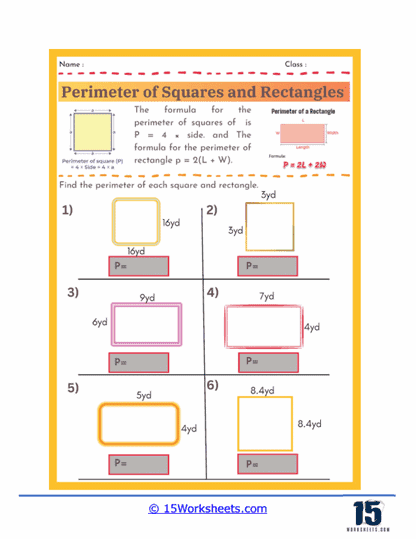
Perimeter of squares and rectangles worksheets serve as a valuable learning tool for students to grasp the concept of measuring the outer boundary of these fundamental geometric shapes. Understanding perimeter is an essential math skill that has real-world applications, from designing floor plans to building fences or framing pictures. These worksheets provide structured exercises that help students practice calculating the total distance around squares and rectangles using given side lengths. By working through various problems, students become more comfortable with the formulas- P = 4s for squares and P = 2(l + w) for rectangles-reinforcing their mathematical foundation in geometry.
How to Find The Perimeter of Squares and Rectangles
Finding the perimeter of squares and rectangles is simple if you remember that the perimeter is the total distance around the shape. It is found by adding up the lengths of all the sides.
For a square, all four sides are the same length. So, to find the perimeter, you just multiply one side by 4.
The formula is: P = 4s (where s is the length of one side.)
For example, if a square has a side length of 5 cm, the perimeter is: P = 4 × 5 = 20 cm
For a rectangle, the opposite sides are equal in length. This means you add the lengths of both the length (l) and width (w) twice.
The formula is: P = 2l + 2w
For example, if a rectangle has a length of 8 cm and a width of 3 cm, the perimeter is: P = 2(8) + 2(3) = 16 + 6 = 22 cm
Example Problem
A rectangular garden has a length of 12 feet and a width of 8 feet. Find the perimeter of the garden.
Step-by-Step Solution:
1. Identify the given measurements:
Length (L) = 12 feet and Width (W) = 8 feet
2. Recall the formula for the perimeter of a rectangle: Perimeter = 2 x (Length + Width)
3. Substitute the given values into the formula: Perimeter = 2 x (12 feet + 8 feet)
4. Add the length and width: 12 feet + 8 feet = 20 feet
5. Multiply the sum by 2 to find the perimeter: Perimeter = 2 x 20 feet = 40 feet
6. Answer: The perimeter of the rectangular garden is 40 feet.
Beyond simple calculations, these worksheets often incorporate word problems and real-life scenarios to deepen students’ comprehension. They encourage critical thinking and problem-solving, as students must apply their knowledge to different contexts, such as finding the missing side length when given the perimeter. Additionally, working with these worksheets helps improve measurement skills, logical reasoning, and attention to detail. Whether used in classrooms, homeschooling environments, or as extra practice at home, perimeter worksheets play a crucial role in building students’ confidence in math while making learning interactive and engaging.
Mathematical Skills Explored
Perimeter of squares and rectangles worksheets cover a range of mathematical skills, including:
Geometry and Spatial Reasoning
Perimeter worksheets focusing on squares and rectangles help students build a strong foundation in geometry and spatial reasoning. Through these exercises, students learn to visualize these shapes in both two-dimensional and real-world contexts, enhancing their ability to recognize patterns and spatial relationships. They practice identifying key attributes of squares and rectangles, such as the number of sides, opposite side congruency, and right angles, which are fundamental to understanding their structure. By developing a deeper comprehension of these geometric properties, students become more adept at analyzing and working with other polygonal shapes in more advanced mathematical concepts.
Measurement
Understanding and accurately measuring the perimeter of squares and rectangles require students to engage with different units of measurement, such as inches, centimeters, and meters. These worksheets help students practice reading rulers, measuring tape, or given numerical values to determine the lengths of sides, reinforcing precision and attention to detail. Additionally, they learn how to convert between different measurement units, strengthening their ability to adapt to real-world applications where conversions are necessary, such as construction, interior design, or architecture. Mastering these measurement skills not only supports their mathematical growth but also prepares them for practical scenarios requiring accurate length estimations.
Algebraic Manipulation
Finding the perimeter of squares and rectangles introduces students to essential algebraic skills by requiring them to apply formulas consistently and correctly. They learn to substitute given values into the standard perimeter formulas- P = 4s for squares and P = 2l + 2w for rectangles-reinforcing their ability to work with algebraic expressions. Through repeated practice, students develop confidence in simplifying expressions, handling arithmetic operations efficiently, and recognizing patterns within perimeter calculations. This process builds a strong algebraic foundation that later extends to more complex topics, such as solving for unknown variables, working with equations, and applying formulas in different mathematical contexts.
Problem-Solving
Solving perimeter-related problems helps students develop critical thinking and logical reasoning skills, which are essential for tackling more advanced mathematical challenges. By working through step-by-step calculations, they learn how to systematically approach problems, breaking them into smaller, more manageable parts. These worksheets often present real-world scenarios, such as fencing a garden or framing a picture, helping students understand the practical applications of perimeter calculations. As they practice, students build resilience in problem-solving, improving their ability to analyze situations, apply relevant formulas, and derive correct answers efficiently.
Real-World Applications
One of the most common real-world applications of perimeter calculations for squares and rectangles is in construction and home improvement projects. For example, when building a fence around a rectangular yard, the total length of fencing material needed is determined by calculating the perimeter of the yard. Similarly, when installing baseboards or trim along the edges of a room, homeowners or contractors must measure the perimeter of the space to ensure they purchase the correct amount of materials. Whether laying down tiles, carpeting a floor, or framing a doorway, understanding how to calculate perimeter ensures accurate measurements and prevents material shortages or excess costs.
Another important use of perimeter calculations is in landscaping and gardening. When designing a rectangular flower bed, walkway, or patio, knowing the perimeter helps determine the quantity of edging material needed to outline the space. Gardeners often need to fence off garden beds to protect plants from animals, and calculating the perimeter allows them to purchase the appropriate amount of fencing. Similarly, outdoor event planners or sports field designers use perimeter measurements to mark boundaries for rectangular areas, such as soccer fields, tennis courts, or festival grounds, ensuring proper space utilization. By accurately measuring and calculating perimeter, professionals can create well-organized and functional outdoor spaces.
In addition to construction and landscaping, perimeter calculations are essential in manufacturing, packaging, and design industries. For instance, when designing rectangular product packaging, companies must measure the perimeter to determine the correct amount of material needed for box edges or wrapping. Retailers who sell picture frames, mirrors, or window panes also use perimeter calculations to ensure their frames or borders fit precisely around the rectangular objects. Even in fashion and textile industries, tailors and designers measure perimeter to cut fabric strips for hemming garments or designing rectangular panels. Whether in industrial production or creative design, knowing how to calculate perimeter is crucial for efficiency, accuracy, and cost-effectiveness in various professional fields.