Triangles Worksheets
About Perimeter of Triangles Worksheets
Perimeter of triangle worksheets are essential tools in mathematics education designed to help students understand and calculate the perimeter of triangular shapes. These worksheets guide students through various methods to determine the perimeter, which is the total distance around the triangle. By working through these worksheets, students develop a deeper understanding of geometric principles, enhance their measurement skills, and improve their problem-solving abilities.
Mathematical Skills Explored
Perimeter of triangle worksheets cover a range of mathematical skills, including:
Identification and Calculation
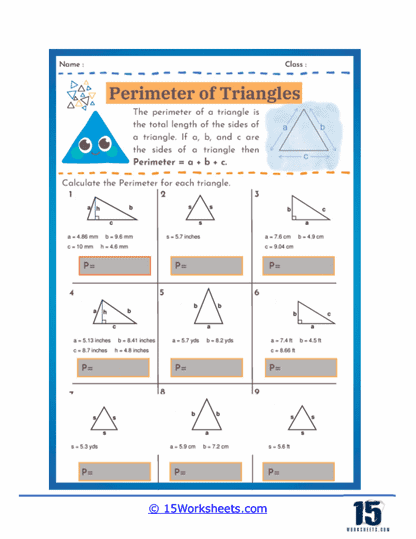
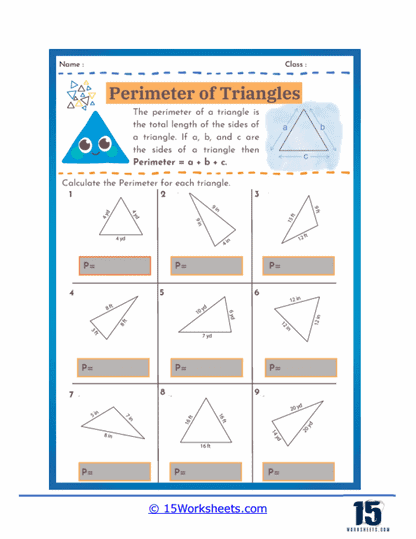
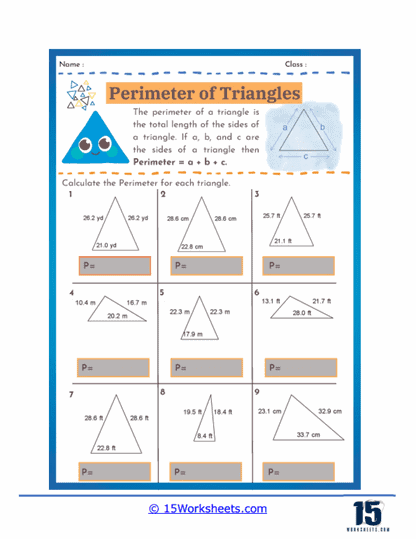
Worksheets on the perimeter of triangles often begin with exercises that help students recognize and identify the essential parts of a triangle. These parts include the sides, which are the line segments forming the triangle, and the vertices, which are the points where the sides meet. Understanding these elements is crucial, as they serve as the foundation for all perimeter-related calculations. In these exercises, students may be asked to label the sides of given triangles using common notation such as a, b, and c, which will later be used in formulas. By thoroughly familiarizing themselves with these elements, students develop a clear understanding of how to measure and organize the given information to solve problems effectively.
Perimeter Formulas
The worksheets introduce students to the standard formula for calculating the perimeter of a triangle, which is expressed as P = a + b + c. In this formula, P represents the perimeter, while a, b, and c correspond to the lengths of the three sides of the triangle. The worksheets provide explanations on why this formula works, emphasizing that the perimeter is simply the total distance around the shape. To reinforce comprehension, students may encounter variations of the formula in different contexts, such as when given a triangle with missing side lengths that they must solve for. Additionally, some worksheets challenge students to apply the formula to triangles of various types—such as scalene, isosceles, and equilateral—to explore how different side lengths affect the final perimeter.
Worked Examples
To help students build confidence in applying the perimeter formula, worksheets often include detailed worked examples. These examples provide a step-by-step breakdown of how to use the formula correctly, from identifying the given values to performing the necessary arithmetic operations. By walking through these problems systematically, students see the logical flow of calculations, which helps prevent common errors such as forgetting to add all the sides or mislabeling the triangle’s parts. Some worked examples also include word problems, where students must extract relevant information from a written description before applying the formula. By analyzing these examples, students gain a better grasp of the problem-solving process and develop the ability to tackle similar problems independently.
Geometry and Spatial Reasoning
Perimeter of triangle worksheets help students develop a strong foundation in geometry by teaching them how to visualize and analyze different types of triangles. Through these exercises, they become familiar with the properties of equilateral, isosceles, and scalene triangles, learning how the lengths of their sides affect their overall shape. Students also gain experience in recognizing congruent and similar triangles, which is essential for more advanced geometry concepts. By engaging with diagrams and hands-on practice, they improve their spatial reasoning skills, enabling them to interpret and construct geometric figures more accurately. This ability to visualize shapes and their dimensions strengthens their understanding of how geometry applies to real-world situations, such as architecture, engineering, and design.
Measurement
These worksheets require students to measure the sides of triangles accurately, reinforcing their ability to use rulers, protractors, and other measuring tools effectively. They learn to work with different units of measurement, such as inches, centimeters, and millimeters, and understand when to use each one based on the problem at hand. Additionally, students practice converting between different units, an essential skill for science, engineering, and everyday applications. Precise measurement is crucial not only for mathematical accuracy but also for developing attention to detail and critical thinking. By consistently working with measurements, students become more confident in their ability to estimate, compare, and analyze lengths in both mathematical and real-world contexts.
Algebraic Manipulation
Finding the perimeter of a triangle involves using algebraic formulas, such as P = a + b + c, where a, b, and c represent the side lengths. Students learn to substitute given values into these formulas and simplify expressions, which reinforces their understanding of basic algebraic operations. As they progress, they encounter problems that require solving for unknown side lengths using algebraic equations, enhancing their ability to work with variables and expressions. These exercises help build a strong foundation for more advanced topics in algebra, such as solving equations, working with inequalities, and understanding functions. By applying algebra in a geometric context, students develop a deeper appreciation for the interconnectedness of mathematical concepts.
Problem-Solving
The process of calculating the perimeter of triangles strengthens students’ problem-solving abilities by encouraging them to apply logical reasoning and systematic approaches. They learn to break down complex problems into smaller, manageable steps, making it easier to identify the necessary calculations and methods. These skills become particularly useful when working with word problems, where students must determine which information is relevant and how to use it effectively. Additionally, perimeter problems often require students to combine multiple mathematical concepts, such as measurement, algebra, and geometry, fostering their ability to think critically and apply knowledge in different contexts. As they gain experience with different problem types, students become more adaptable and confident in tackling a wide range of mathematical challenges.
Real-World Applications
Many worksheets incorporate real-world applications to demonstrate the practical importance of calculating the perimeter of triangles. These applications might involve scenarios such as determining the amount of fencing needed for a triangular garden, estimating the borders of triangular plots of land, or measuring the edges of triangular road signs. By engaging with these realistic problems, students understand how mathematical concepts extend beyond the classroom and into everyday situations. Some worksheets may also introduce interdisciplinary connections, such as using perimeter calculations in architecture, engineering, or even sports fields. Applying their knowledge to real-life contexts helps students see the relevance of perimeter calculations and strengthens their problem-solving skills in meaningful ways.
Perimeter of Triangles Example Problem
A triangle has sides of lengths 5 cm, 7 cm, and 9 cm. Calculate the perimeter of the triangle.
Step-by-Step Solution:
1. Identify the lengths of the sides of the triangle:
a. Side a = 5 cm
b. Side b = 7 cm
c. Side c = 9 cm
2. Write down the formula for the perimeter of a triangle:
a. Perimeter = a + b + c
3. Substitute the lengths of the sides into the formula:
Perimeter = 5 cm + 7 cm + 9cm
4 . Calculate the sum:
Perimeter = 21cm
The perimeter of the triangle is 21 cm.