Factor Tree Worksheets
About These 15 Worksheets
Factor Tree Worksheets are specialized educational resources designed to assist students in comprehending the process of prime factorization, a foundational concept in number theory and algebra. Just as trees have branches that divide into smaller branches, a factor tree illustrates how a number can be divided into its prime factors. Let’s delve deeper into the world of Factor Tree Worksheets, the types of exercises they contain, and their implications for fostering stronger mathematical skills.
The Types of Problems
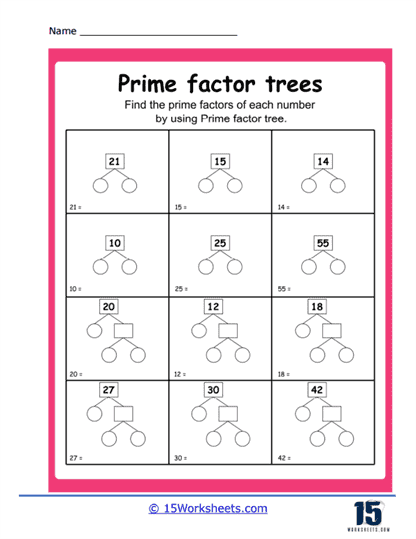
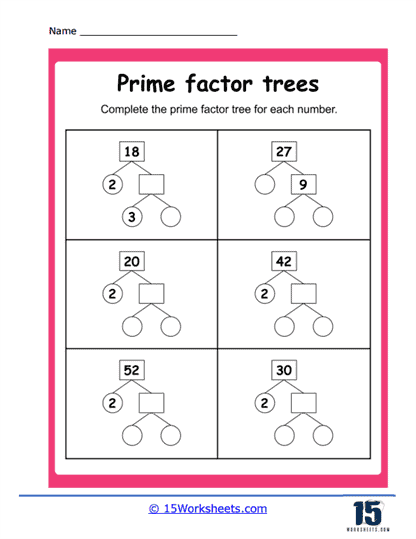
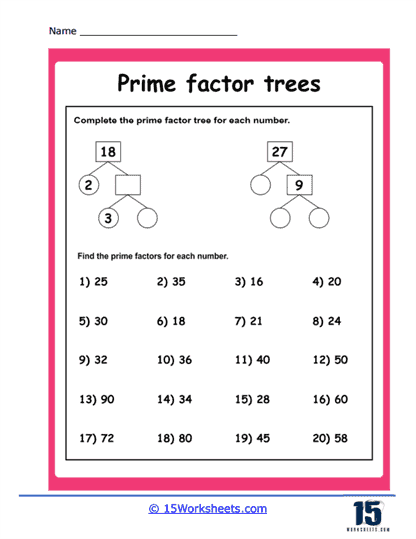
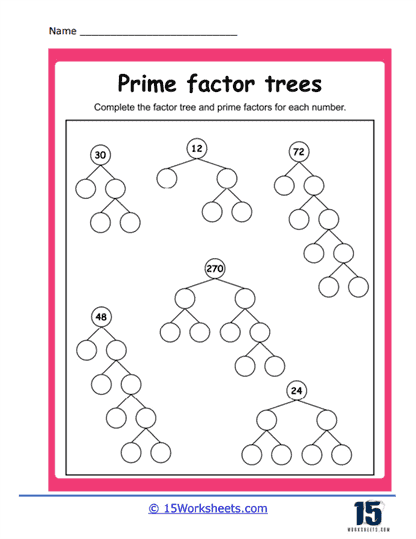
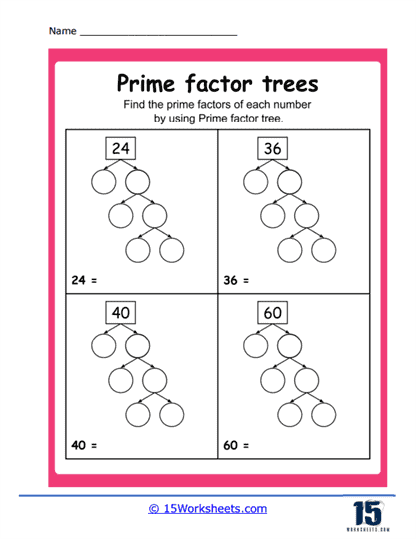
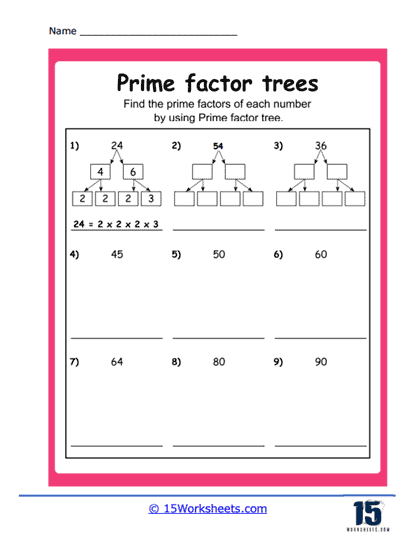
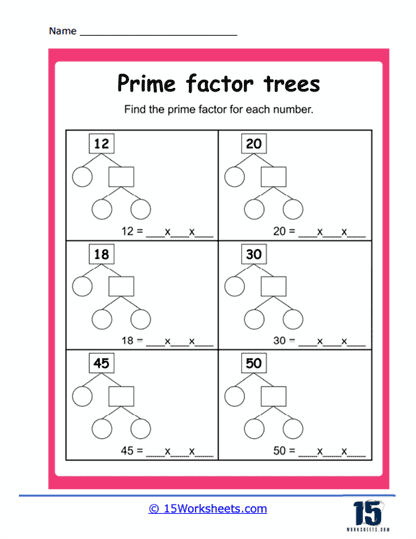
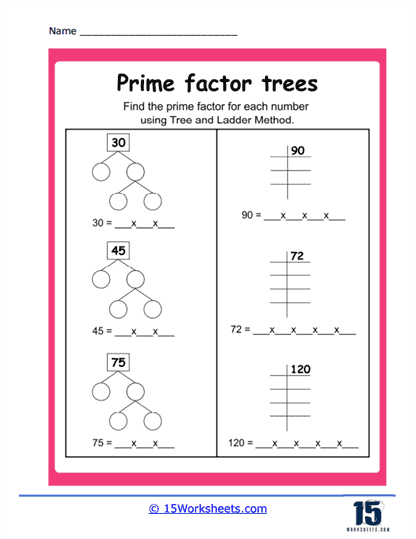
Basic Prime Factorization – These exercises typically begin with a composite number, and students are required to break it down step-by-step into its prime factors using a tree diagram. For example, for the number 36, the factor tree would have branches dividing it into 6 and 6, and then further into 2 and 3, showing that 36 = 2 x 2 x 3 x 3.
Given Prime Factors – Instead of a straightforward factorization, students are given specific prime numbers and are tasked with determining which composite numbers can be formed using these primes.
Multiple Choice Questions – These exercises present a composite number and several potential factor tree diagrams or prime factorization answers. Students must select the correct option.
Reverse Factor Trees – In these exercises, the prime factorization of a number is provided, and students must work backward to determine the original composite number.
Factor Trees with Exponents – These exercises incorporate the use of exponents in the final answer. For example, for the number 72, the prime factorization is 23 x 32.
Mixed Review – A combination of the above exercise types, helping students solidify their understanding and improve their flexibility with factor trees.
What You Can Learn From These Worksheets
Foundation in Number Theory – Understanding the prime components of numbers is a fundamental concept in number theory. It forms the basis for concepts such as greatest common divisor (GCD) and least common multiple (LCM).
Algebraic Application – In algebra, factorization skills extend to polynomial expressions. A strong grounding in numerical factorization can ease this transition.
Enhanced Problem-solving Skills – Factor Tree Worksheets foster analytical thinking, as students learn to dissect numbers methodically. This structured thinking can be applied in more complex mathematical problems.
Improved Multiplication and Division Skills – As students break down numbers, they engage in repeated division and recognize multiplication patterns, reinforcing these core arithmetic operations.
Boosted Confidence – Mastery of factor trees can enhance a student’s confidence in tackling more advanced mathematical concepts, creating a positive feedback loop for learning.
Understanding Mathematical Structures – Factor trees illuminate the hierarchical structure inherent in numbers. This understanding can help students in areas like modular arithmetic, cryptography, and advanced computational techniques.
In the Real World
Understanding prime factorization and the ability to break down numbers may seem abstract, but they have numerous real-life applications:
Financial Literacy – Factors and multiples come into play when discussing interest rates, loans, and investments. Being able to break down and understand these numbers can assist in making informed financial decisions.
Cooking and Baking – Often, recipes need to be scaled up or down. Prime factorization can help in understanding ratios and proportions essential for such adjustments.
Home Improvement – When tiling a floor or determining the number of paint cans required for a room, understanding factors can help in making efficient and cost-effective decisions.
Planning and Organizing Events – Whether determining seating arrangements for guests (factors of a table arrangement) or buying supplies in bulk, a grasp of numbers and their factors can be incredibly helpful.
Shopping – Recognizing patterns and factors can assist in determining deals, understanding bulk pricing, or making quick mental calculations about discounts.
Gaming – Many strategy games, both digital and board-based, require players to calculate odds, understand numerical patterns, or make decisions based on numbers. Prime factorization can play a subtle role in making optimal choices.
Environmental Conservation – When trying to reduce waste or energy usage, understanding numbers and their breakdown can help in devising efficient strategies for conservation.