Commutative Property Worksheets
About These 15 Worksheets
These worksheets were developed to help students understand and apply the commutative property of addition in mathematical operations. The commutative property states that numbers can be added in any order and the sum will remain the same. In other words, if you have two numbers, A and B, then A + B will always equal B + A.
They contain a diverse range of exercises tailored to help students understand and apply the commutative property, thereby improving their basic math skills, developing their problem-solving abilities, and building a solid foundation for future mathematical learning.
Types of Exercises
On such worksheets, students typically encounter a variety of exercises that reinforce this concept. These exercises can take several forms:
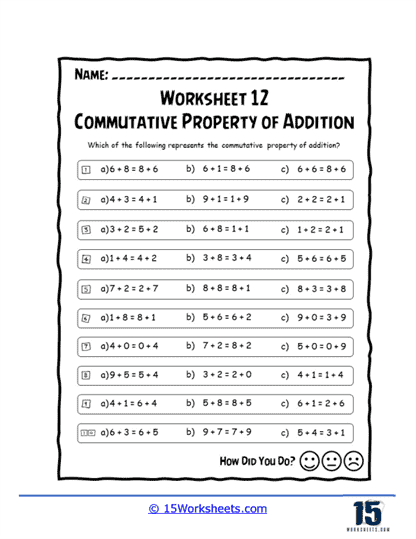
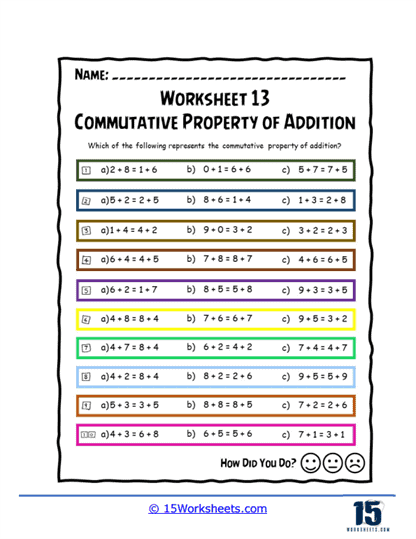
Basic Number Swaps – The most straightforward type of exercise asks students to simply swap the order of addends and verify that the sum remains unchanged. For example, the worksheet might present 3 + 5 and prompt the student to rewrite it as 5 + 3, then perform both additions to see that they equal 8.
Fill in the Blank – These exercises leave one addend blank, and the student must fill in the blank to make two true addition sentences. For example, if the worksheet says 2 + ___ = ___ + 2, the student would fill in both blanks with the same number.
Matching Pairs – In this type of exercise, students might be presented with a column of addition equations and a column of jumbled sums. Their task is to match each equation with its correct sum, emphasizing that regardless of the order of addends, the sums will match.
Error Identification – Some worksheets may present students with a series of equations, some of which incorrectly apply the commutative property. Students must identify and correct these mistakes, reinforcing their understanding of the property. These exercises present equations with missing numbers that students need to find. For instance, an equation might read 4 + ___ = ___ + 6, and students must figure out that the missing number is the same in both blanks.
Create Your Own Equation – Students may be asked to create pairs of their own addition sentences using a given set of numbers, demonstrating their understanding by actively constructing examples.
The Benefits
This collection of worksheets can significantly enhance students’ understanding of basic math operation skills in several ways:
Enhanced Flexibility in Thinking – By repeatedly practicing the commutative property, students learn that the order of addends does not affect the sum. This foundational understanding is crucial for flexible thinking in math, allowing them to manipulate and rearrange numbers to simplify complex problems. Worksheets that require students to identify errors or create their equations help develop critical problem-solving skills. Students learn to check their work for accuracy and to approach problems from different angles.
Increased Speed and Efficiency – As students become more familiar with this property, they can perform additions more quickly and with greater confidence. Knowing that they can add in any order lets them choose the most efficient way to combine numbers, particularly when dealing with mental math.
Preparation for Advanced Concepts – The commutative property is not only applicable in basic addition but also forms the basis for understanding more advanced mathematical concepts such as the distributive property and algebraic equations. By working on word problems that incorporate the commutative property, students can connect mathematical operations to real-world situations, reinforcing the practical value of what they are learning.
Confidence in Mathematics – As students master the commutative property, they often gain confidence in their math abilities. This confidence can lead to a more positive attitude toward math and a willingness to engage with more challenging problems.
What Is The Commutative Property of Addition?
The Commutative Property of Addition is a fundamental principle in mathematics, particularly within the field of algebra. It is one of the basic properties of numbers and operations that underpins the entire structure of arithmetic and algebra. This property states that the order in which two numbers are added does not affect the sum. In other words, if you have two addends (the numbers being added), switching their places does not change the result of the addition.
Mathematically, the Commutative Property of Addition is expressed as: a + b = b + a
Here, a and b are variables that represent any real numbers. The ‘+’ sign denotes the operation of addition. According to this property, for any two real numbers a and b, the sum remains the same regardless of the order of the addends (addition parts).
The property is called ‘commutative’, stemming from the word ‘commute’, which means to move around or to change place. In this context, it implies that addends can ‘move around’ or change places without affecting the outcome of the operation.
The Commutative Property of Addition has profound implications:
It allows for flexibility in computation, enabling one to rearrange terms to simplify the process of addition.
It is essential for the development of a deeper understanding of the structure of the number system.
It lays the groundwork for algebraic manipulations where the ability to rearrange and combine like terms is fundamental.
Let’s look at two examples to see the Commutative Property of Addition in action:
Example 1: Simple Numerical Addition
Suppose you have the numbers 3 and 5. According to the Commutative Property of Addition, if you add 3 and 5, you will get the same result as when you add 5 and 3.
3 + 5 = 8
5 + 3 = 8
In both cases, the sum is 8. This illustrates that the order of the numbers does not affect the result of the addition.
Example 2: Addition Involving Variables
The Commutative Property holds true not just for concrete numbers but also for algebraic expressions. Consider the expressions x and y, where x and y are variables that can represent any number.
x + y = y + x
This equation tells us that no matter what values x and y take on, the sum will be the same whether x is added to y or y is added to x. For instance, if x = 10 and y = 15, then:
10 + 15 = 25
15 + 10 = 25
Both expressions yield the same sum, 25, demonstrating the commutative nature of the addition of these variables.