Scientific Notation Worksheets
All About These 15 Worksheets
Scientific notation is a mathematical method used to express very large or very small numbers in a more manageable form, which is especially useful in fields like science and engineering. This collection of worksheets is designed to help students develop fluency in this area through a variety of exercises, making it an excellent tool for middle and high school students who are ready to deepen their understanding of algebra and mathematical concepts.
What’s Inside the Collection
These PDF-format worksheets provide a versatile and convenient way for students to practice scientific notation. The format allows for easy viewing, downloading, and printing, making it simple for educators and students to access them anytime. The variety of exercises included ensures that students are not only introduced to scientific notation but are able to practice it in multiple contexts.
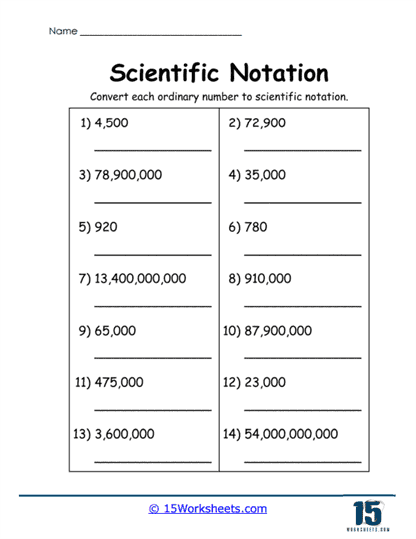
Converting Ordinary Numbers to Scientific Notation
The first set of worksheets, as seen in some of the attached images, focuses on converting large and small ordinary numbers into scientific notation. For example, students might be asked to express numbers like 4,500 or 78,900,000 in scientific notation. These tasks help students understand how to shift decimal points and write numbers using powers of ten. They also reinforce the concept of significant figures, showing students how to handle both large and small numbers efficiently.
Similarly, worksheets are included that ask students to convert small decimals, such as 0.0062 or 0.000345, into scientific notation. These exercises serve to solidify students’ understanding of negative exponents and how they represent very small numbers in scientific notation.
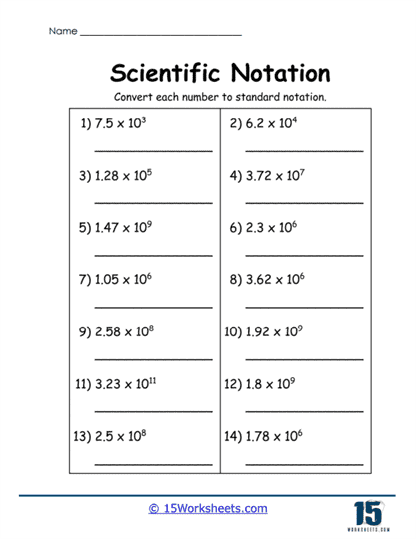
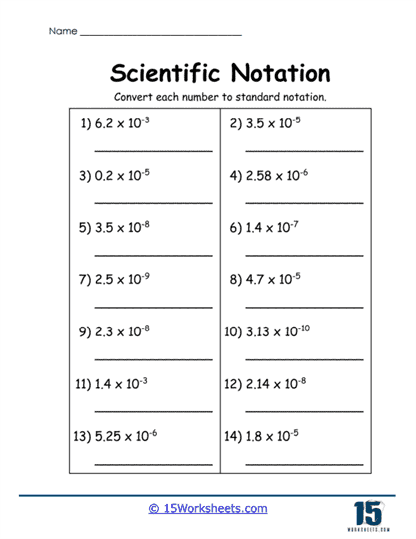
A balanced approach is achieved with worksheets that take the reverse approach, asking students to convert numbers from scientific notation back to their standard form. Examples like 7.5 × 103 or 1.28 × 105 are given, and students are required to expand these into their full numerical form. This reinforces their comprehension of how powers of ten work and ensures they can move fluently between the two notational systems.
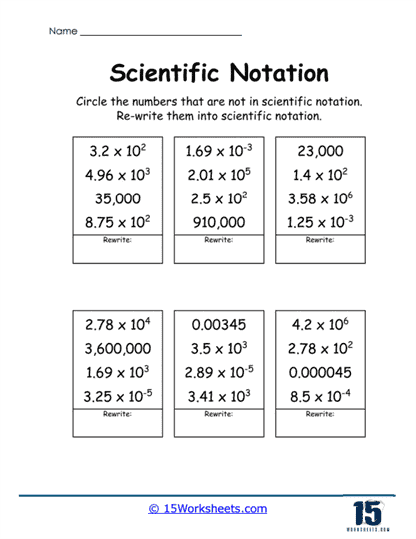
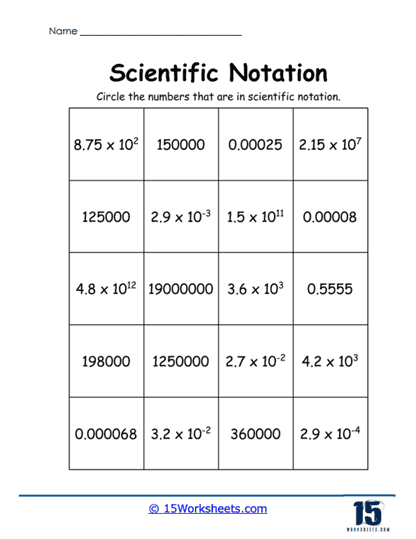
Comparing Numbers in Scientific Notation
An interesting variation in the worksheets focuses on comparing numbers written in scientific notation. Students are asked to use symbols like >, <, or = to compare values such as 5.5 × 106 and 7.3 × 103. This task builds a deeper understanding of exponents and helps students visualize the magnitude of different numbers. Comparing large and small numbers in this way also prepares students for more advanced mathematical operations in scientific and real-world contexts.
Operations
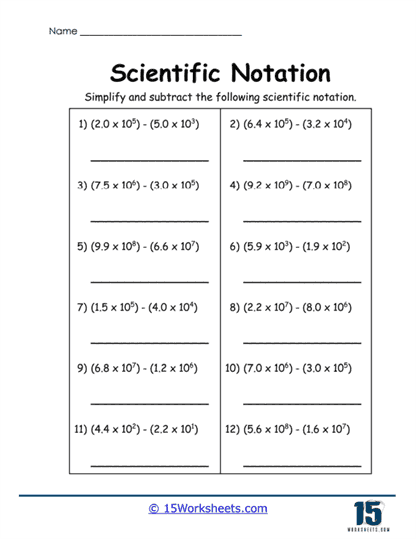
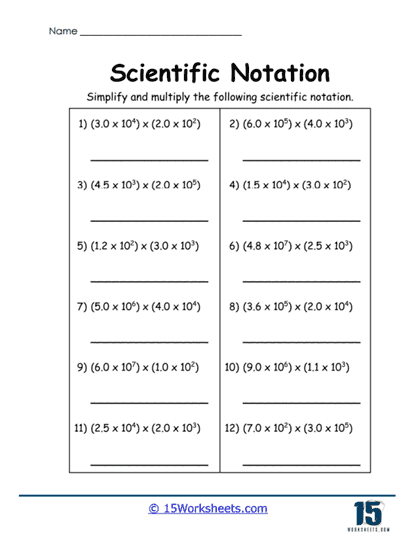
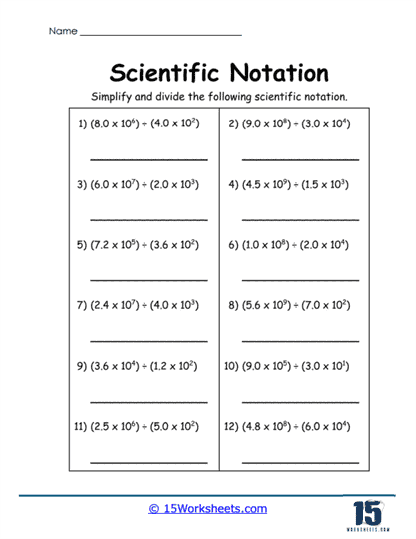
More advanced worksheets included in the collection ask students to add and subtract numbers written in scientific notation. Problems like (3.2 × 105) + (4.5 × 105) or (2.8 × 107) – (3.4 × 107) push students to apply their understanding of both scientific notation and basic arithmetic. These exercises are excellent for reinforcing concepts related to exponents, significant figures, and order of magnitude. Students will also be tasked with multiplying and dividing numbers written in scientific notation, applying rules for exponents and ensuring their final answers are expressed correctly.
The PDF format of these worksheets makes them easily accessible and practical for both teachers in a traditional classroom setting and homeschoolers managing multiple subjects. Teachers can download, print, and distribute the worksheets to their students, ensuring that they have a ready-made resource for teaching or reinforcing this key algebraic concept.
For homeschoolers, this collection provides an invaluable set of tools for guiding independent study. The clear instructions and diverse problem sets ensure that students can practice at their own pace, revisiting difficult concepts as needed. Furthermore, the range of activities-from simple conversions to more complex operations like adding and subtracting scientific notation-allows students to gradually build their skills without feeling overwhelmed.
What is Scientific Notation?
Scientific Notation is a mathematical way of expressing very large or very small numbers in a simplified, standardized form using powers of ten. In scientific notation, a number is written as the product of two components: a coefficient (a number between 1 and 10) and a power of ten. For example, the number 4,500 in scientific notation is written as 4.5 x 103, which represents 4.5 x 1,000 = 4,500. Similarly, a small number like 0.0062 can be expressed as 6.2 x 10-3, where the negative exponent indicates that the decimal point is moved three places to the left. This system allows for a more compact representation of numbers that are too large or too small to easily work with in their standard form.
The Basic Structure of Scientific Notation
The general format for scientific notation is a x 10n, where a is the coefficient and n is the exponent. The coefficient must be a number between 1 and 10, and the exponent n tells you how many places to move the decimal point. A positive exponent indicates that the decimal point moves to the right, representing a large number, while a negative exponent moves the decimal point to the left, representing a small number. For example, 7.3 x 105 is equal to 730,000, whereas 7.3 x 10-5</sup is equal to 0.000073.
This system simplifies calculations and the comparison of magnitudes because scientists and mathematicians can focus on the exponents rather than writing out long strings of digits. It becomes easier to handle numbers with many zeros, which would otherwise be cumbersome or error-prone to write in full.
Real-World Applications
Scientific notation is used extensively in various scientific fields because many measurements and quantities encountered in science are either extremely large or extremely small. For instance, in astronomy, the distances between stars and galaxies are vast, often measured in trillions of kilometers. Instead of writing such large numbers in their standard form, which would involve many zeros, astronomers use scientific notation. The distance from Earth to the Sun, for example, is about 150,000,000 kilometers, which can be more conveniently expressed as 1.5 x 108kilometers in scientific notation.
Similarly, in physics and chemistry, scientific notation is essential for dealing with very small quantities, such as the size of atoms or the mass of subatomic particles. The diameter of a hydrogen atom is approximately 1.06 x 10-10 meters, which is much easier to write and comprehend than the standard form, 0.000000000106 meters. These tiny numbers would be extremely awkward to work with in everyday calculations without scientific notation, as the risk of error increases when writing out many decimal places.
Why is Scientific Notation Helpful?
The main advantage of scientific notation is that it simplifies both the expression and manipulation of very large or very small numbers. For one, it reduces the number of digits one has to work with, cutting down on potential errors when writing or reading numbers. For instance, imagine calculating the product of 2.5 x 107 and 3.4 x 105 without scientific notation. You would have to multiply 25,000,000 by 340,000, which would be cumbersome and prone to mistakes. In scientific notation, however, you can quickly multiply the coefficients (2.5 and 3.4) and add the exponents, making the process much more efficient.
Scientific notation also makes it easier to compare magnitudes. In fields like engineering or geology, professionals often need to compare vastly different quantities. For example, comparing the mass of the Earth (5.97 x 1024 kilograms) to the mass of a single bacterium (1.0 x 10-12 kilograms) would be nearly impossible using standard notation, but with scientific notation, the difference in the powers of ten (24 versus -12) immediately shows the immense scale difference.
Scientific notation is also fundamental in the world of computing, particularly when dealing with data science, graphics, and large-scale computations. Computers can handle numbers more effectively when they are expressed in terms of powers of ten because it optimizes the way data is stored and processed. For example, floating-point arithmetic, which is used in most computer systems to represent real numbers, is closely related to scientific notation. It allows computers to perform calculations on very large or very small numbers without sacrificing accuracy or requiring an impractical amount of memory.
In fields like economics, scientific notation is useful for expressing large financial figures, such as national debts, gross domestic products (GDPs), or the total value of global markets. For example, the U.S. national debt is over 31 trillion dollars, which can be written as 3.1 x 1013 dollars. This form of notation not only makes it easier for analysts and economists to work with such large numbers, but it also helps communicate these figures more efficiently in reports and studies.
In finance, scientific notation is sometimes used to express very small quantities, such as interest rates or the value of stocks that fluctuate by tiny amounts. While decimal form is common in finance, scientific notation becomes more relevant in fields like high-frequency trading, where extremely small time intervals and price changes must be considered.
In medicine and biology, scientists frequently work with tiny measurements, such as the size of cells, bacteria, or even molecules of DNA. Scientific notation is critical when quantifying substances like hormones or medications in blood, where concentrations can be minuscule, often in the range of nanograms or picograms. For instance, a hormone concentration might be measured as 3.5 x 10-9 grams per milliliter, making it easier to handle and communicate than its decimal counterpart, 0.0000000035 grams per milliliter.