Direct And Inverse Variation Worksheets

All About These 15 Worksheets

This collection is a comprehensive set of algebraic activities designed to help students master the key concepts of direct and inverse variation. Whether used in classrooms, homeschools, or tutoring sessions, these worksheets offer engaging, varied, and progressive exercises that cater to a range of student skill levels. They serve as excellent practice for building a deeper understanding of how variables interact in both direct and inverse relationships, which is essential for students as they develop their algebraic reasoning skills.

A Look At The Individual Worksheets

With Direct Equation Solver and Equation Variation Decider, learners don their math goggles and determine whether a relationship is direct, inverse, or just straight-up confused. These sheets are the algebraic version of speed dating-you meet an equation, figure out if it’s “the one” (direct or inverse), and then solve it like you’re trying to impress its parents.

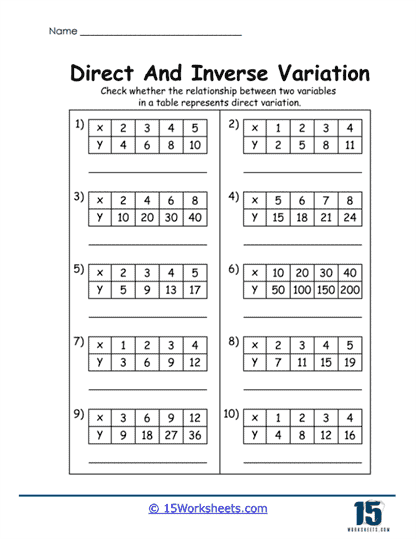
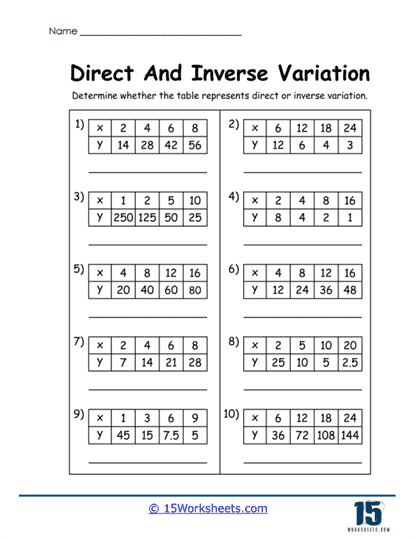
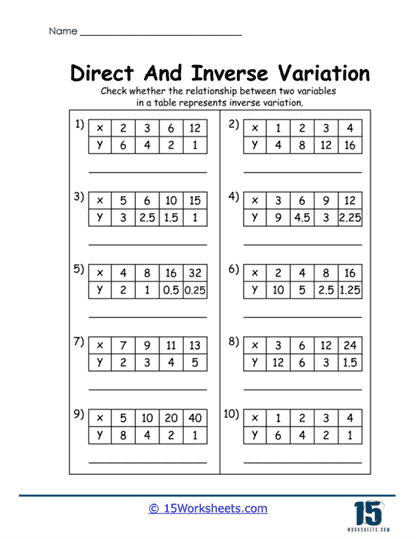
Once you’ve locked down your equation-identifying instincts, it’s time to enter the realm of tables-where data doesn’t just sit around, it tells a story. In Direct Variation Table Hunt and Inverse Variation Table Spotter, students must sift through rows and columns like number detectives, sniffing out patterns faster than Sherlock Holmes with a graphing calculator. Then there’s Missing Table Values, which sounds like the saddest dinner party ever, but is actually an exercise in logical completion. If you’ve ever wanted to feel like a magician pulling answers from a hat (or a two-way table), this is your time to shine.

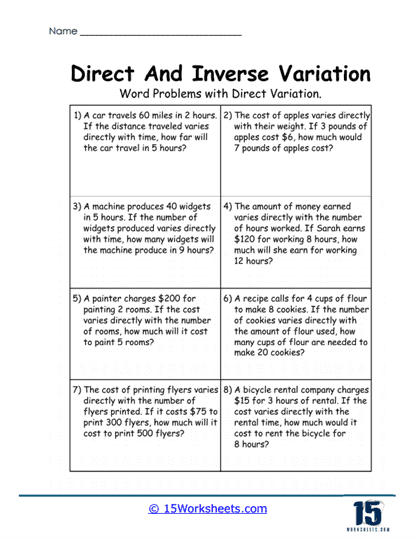
Just when students start thinking they’ve got this whole variation thing down, the worksheets throw in some real-life twists with Direct Word Problems and Inverse Word Problems. Here, math gets a bit personal. Now the questions are about things like how fast Billy finishes mowing lawns or how the number of people sharing a pizza impacts your slice count. It’s practical, a little bit dramatic, and a fantastic reminder that math exists outside of textbooks too. These worksheets don’t just make students solve problems-they make them live them. (Hopefully with fewer pizza-related arguments.)

To keep things spicy, students are challenged to dig deeper into the mysterious constants that make variation tick. Direct Variation Constants, Inverse Variation Constants, and Constant Calculation invite learners to decode the magical multiplier or divisor that links all the terms together like some kind of algebraic glue. It’s the part of the problem that rarely gets the spotlight, but without it, everything falls apart-kind of like forgetting your Netflix password or misplacing your coffee in the morning.

The culmination of this brainy math odyssey arrives with the grand finale of worksheets: Direct Value Finder, Inverse Value Solver, Variation Identifier, and Variation Challenge. This is where students combine everything they’ve learned-equations, tables, real-world logic, and the elusive constant-to solve complex puzzles and strut their mathematical stuff. Think of it as the Algebra Olympics: everyone’s flexing formulas, lifting variables, and going for the gold in logical reasoning. And when they finally master these, they don’t just understand variation-they own it.

What is Direct And Inverse Variation?

Direct and inverse variation concepts have practical applications in everyday life, often in ways that teenagers might not immediately recognize but experience frequently. These algebraic principles are tools that can help them understand relationships between different quantities and make predictions about outcomes based on changes in related factors. Whether it’s in school, during hobbies, or while making decisions about time and resources, understanding how direct and inverse variation works can help teenagers solve problems and make better choices.

Direct Variation in Daily Life

One of the simplest examples of direct variation in a teenager’s life is speed and distance when traveling. For instance, if a teen is riding a bike or driving a car, the distance traveled is directly proportional to how fast they are going and how long they keep moving. If they travel at a constant speed, the longer they ride, the farther they go, which is a perfect example of direct variation: the distance increases as time increases at the same rate. By understanding this, teenagers can better plan their time, estimating how long it will take them to get from one place to another.

Another example is in budgeting and allowances. If a teenager has a part-time job that pays by the hour, the amount of money they earn is directly proportional to the number of hours they work. If they work more hours, they earn more money, making this a direct variation scenario. By understanding this, they can plan their work schedules to save for a purchase or meet their financial goals, using direct variation to calculate how many hours they need to work to reach a specific earning target.

Inverse Variation in Real-World Contexts

Inverse variation is also present in everyday situations, often in terms of balancing competing factors. One example teenagers might encounter is when working on a group project in school. If the amount of time needed to complete a task is inversely proportional to the number of people working on it, then the more team members there are, the less time it should take to finish the project. However, as group size increases, each person’s contribution might decrease, so balancing this variation can help teens better manage group dynamics and optimize their efforts.

Another area where inverse variation comes into play is in sharing resources, such as dividing pizza among friends. If the number of slices each person gets is inversely proportional to the number of people, the more people there are, the smaller each share becomes. Understanding this relationship can help teenagers grasp how resources like time, money, and materials are shared or distributed, making them more mindful of how these things change depending on the circumstances.

Time Management and Proportions

Teenagers can also use these concepts to manage their schedules more effectively. For example, time management relies on understanding both direct and inverse variation. If they have a set amount of time to study for a test, the amount of time they spend on each subject might vary inversely with the number of subjects they need to cover. In contrast, if they need to prepare for an event and spend more time practicing a skill, their proficiency in that area will likely increase proportionally to the effort they put in-another form of direct variation. Recognizing these relationships helps teens better allocate their time, balancing multiple tasks or improving specific skills efficiently.

Fitness and Health

Direct and inverse variation principles are also useful in health and fitness. For instance, in exercise, a teenager’s calorie burn is directly proportional to the intensity and duration of the workout. The harder or longer they exercise, the more calories they burn. Conversely, if they split their workout time across multiple activities, the effort dedicated to each individual activity might decrease. By understanding these variations, teens can tailor their workouts to meet fitness goals, optimizing their exercise routines based on the desired outcomes.

Learning and Growth

In academic contexts, the time spent studying is often directly proportional to a student’s academic success. More time dedicated to practicing problems or understanding concepts tends to lead to better results on tests or assignments. However, this relationship can also have diminishing returns if time is not managed wisely. For instance, a teenager might notice that as they increase the number of hours studying without breaks (inverse variation with breaks), their ability to focus decreases. Recognizing this inverse variation helps them plan for better breaks and study sessions, ensuring that they remain productive.