Decimal Partitioning Worksheets
About These 15 Worksheets
These worksheets are designed to help students develop a solid understanding of decimals by breaking down or “partitioning” decimal numbers into their component parts. These worksheets are invaluable for reinforcing key concepts in decimal arithmetic, number sense, and place value. In this discussion, we’ll explore what decimal partitioning worksheets typically include, the math skills they address, and how they contribute to a student’s overall mathematical development.
Components of Decimal Partitioning Worksheets
Decimal partitioning worksheets usually consist of various exercises that help students manipulate and understand decimals in different ways. Here are the primary components you can expect to find:
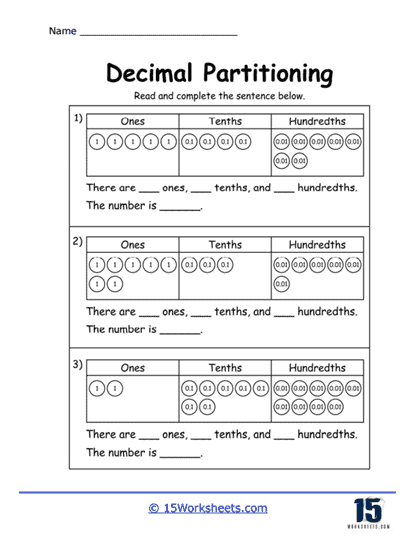
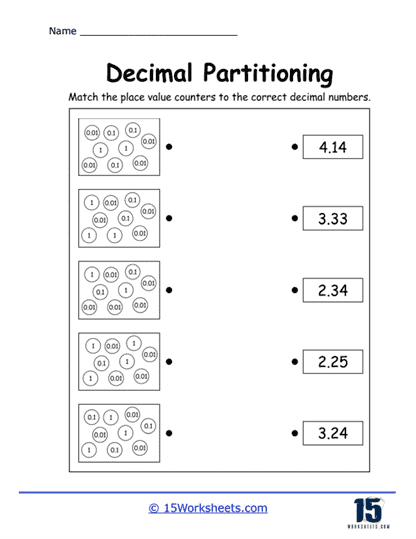
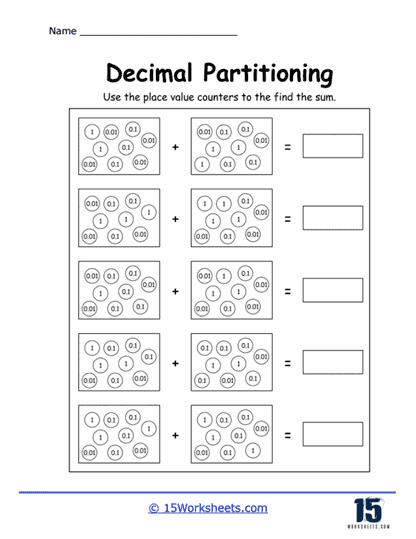
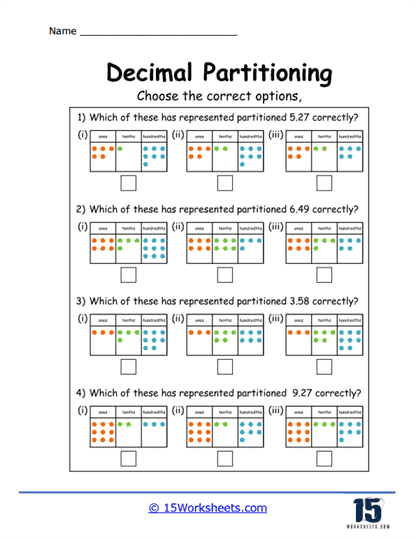
Decimal Place Value Exercises – Decimal place value exercises are foundational in decimal partitioning worksheets. These exercises require students to identify the place value of digits in decimal numbers, such as tenths, hundredths, and thousandths. For example, in the number 3.456, students must recognize that 4 is in the tenths place, 5 in the hundredths place, and 6 in the thousandths place.
This type of exercise reinforces the concept that each digit in a decimal number has a specific value depending on its position relative to the decimal point. Understanding place value is critical because it underpins all operations involving decimals, including addition, subtraction, multiplication, and division.
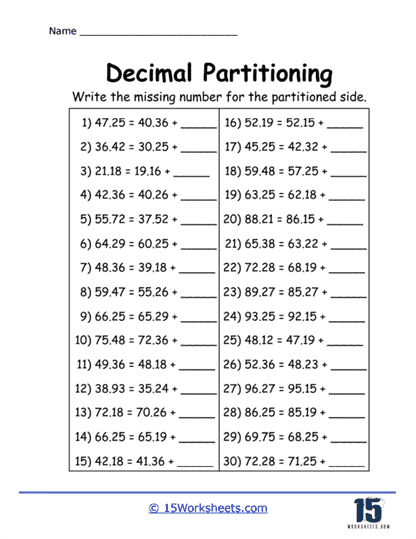
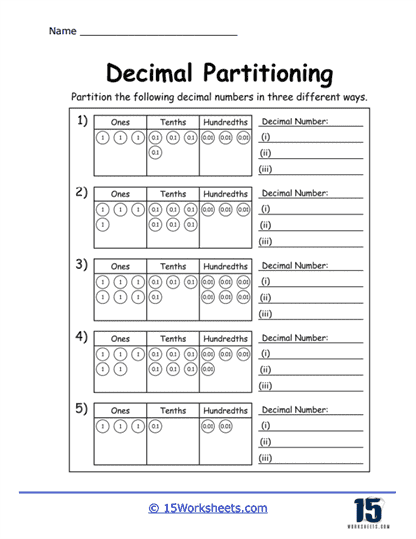
Expanded Form Exercises – Another common feature of decimal partitioning worksheets is exercises on writing decimals in expanded form. In these exercises, students break down a decimal into its component parts. For example, the number 2.347 would be written in expanded form as 2 + 0.3 + 0.04 + 0.007.
These exercises help students understand the concept of decomposing numbers, which is a key skill in both arithmetic and algebra. It also allows students to see how each digit contributes to the overall value of the number, reinforcing the importance of place value.
Comparing and Ordering Decimals – Our worksheets include problems where students must compare and order decimal numbers. These exercises might involve determining which of two decimals is greater, or arranging a list of decimals in ascending or descending order.
To solve these problems, students must accurately compare the place values of digits in different decimal numbers. This skill is crucial not only for understanding decimals but also for real-life applications like comparing prices, measurements, and other numerical data.
Rounding Decimals – Rounding decimals is another typical component of these worksheets. Students are asked to round decimal numbers to the nearest whole number, tenth, hundredth, or thousandth. For instance, they might round 5.678 to 5.68 if rounding to the nearest hundredth.
Rounding is a practical skill that students will use frequently outside the classroom. It’s essential for estimating calculations, understanding significant figures in science, and simplifying numbers in everyday situations.
Adding and Subtracting Decimals – Decimal partitioning worksheets usually include exercises on adding and subtracting decimals. These problems require students to align the decimal points of the numbers they are adding or subtracting, which helps them maintain the correct place value.
Adding and subtracting decimals is a vital skill in math, as it lays the groundwork for more complex operations involving decimals and fractions. It’s also a necessary skill for managing money, as students will often encounter decimals when dealing with dollars and cents.
Multiplying and Dividing Decimals – More advanced worksheets might include problems on multiplying and dividing decimals. When multiplying, students learn to multiply as if the numbers were whole numbers and then place the decimal in the correct position in the product. When dividing, they may need to convert the divisor to a whole number by moving the decimal point and doing the same in the dividend.
These operations require a deep understanding of place value and are crucial for more advanced math concepts, such as solving equations and working with scientific notation. They also have real-world applications, such as in measurements, finance, and scientific calculations.
Decimal Word Problems – Decimal partitioning worksheets often feature word problems that involve decimals. These problems require students to apply their understanding of decimals in real-life contexts. For example, a problem might involve calculating the total cost of items purchased at a store or determining the distance traveled when given a speed and time.
Word problems help students develop critical thinking and problem-solving skills. They learn to translate a real-world situation into a mathematical equation and then solve it, which is an essential skill not just in math, but in everyday life.
Decimal to Fraction Conversion – Another key component is converting decimals to fractions and vice versa. Students might be asked to express a decimal like 0.75 as a fraction (which would be ¾) and simplify it if necessary. Conversely, they might convert a fraction like 1/8 into a decimal.
This skill is fundamental because it bridges the gap between decimals and fractions, two key areas in mathematics. Understanding this relationship is crucial for students as they progress into algebra and more advanced math topics.
Visual Representations of Decimals – Some worksheets include visual aids, such as grids or number lines, to help students better understand decimal concepts. For example, a worksheet might include a grid divided into 100 parts, where students can shade in a portion to represent a decimal like 0.35.
Visual representations are particularly helpful for students who struggle with abstract concepts. They provide a concrete way to see how decimals represent parts of a whole, making the concept more accessible and easier to grasp.
Decimal Patterns and Sequences – Finally, some worksheets might challenge students to recognize and continue patterns or sequences involving decimals. For example, students might be asked to find the next number in a sequence like 0.5, 0.55, 0.6, 0.65, etc.
Identifying patterns and sequences helps students develop their analytical and reasoning skills. It also reinforces their understanding of place value and how decimals can incrementally increase or decrease.
Skills Taught by These Worksheets
Each of the components described above teaches specific math skills that are essential for students’ mathematical development. Here’s a closer look at these skills:
1. Place Value Understanding – Almost all exercises on decimal partitioning worksheets reinforce the concept of place value. Whether students are identifying place values, expanding numbers, or comparing decimals, they are continually reminded that the position of a digit determines its value. This understanding is foundational not just for decimals but for all number operations.
2. Arithmetic Operations with Decimals – Adding, subtracting, multiplying, and dividing decimals are crucial arithmetic skills taught through these worksheets. These operations are vital for everyday tasks, such as handling money, measuring objects, and performing calculations in science and engineering.
3. Number Sense and Estimation – By rounding decimals and solving word problems, students develop number sense and estimation skills. These skills help students make reasonable guesses and simplify complex problems, which are important abilities both in and out of the classroom.
4. Fraction-Decimal Relationship – Converting between decimals and fractions helps students see the relationship between these two types of numbers. This understanding is critical as students move into higher-level math, where they will need to work fluently with both fractions and decimals.
5. Problem-Solving and Critical Thinking – Word problems and pattern recognition exercises teach students how to apply their knowledge in practical situations. These problems require students to think critically, analyze information, and devise strategies for finding solutions-skills that are invaluable in all areas of life.
6. Visualization and Conceptual Understanding – Visual aids on worksheets help students develop a conceptual understanding of decimals. By seeing decimals represented on grids or number lines, students can better grasp the idea that decimals represent parts of a whole, making the concept more tangible and less abstract.
From place value identification to arithmetic operations, from word problems to visual representations, these worksheets cover all aspects of decimal numbers. By working through these worksheets, students not only master the mechanics of working with decimals but also develop critical thinking, problem-solving, and analytical skills that will serve them well throughout their education and beyond. Decimal partitioning is more than just a mathematical exercise; it’s a key part of building a strong mathematical foundation that students will rely on throughout their academic and everyday lives.