AB Patterns Worksheets
About These 15 Worksheets
They not only introduce students to the fundamental concept of patterns but also play a crucial role in developing numeracy, problem-solving skills, critical thinking, and a keen attention to detail. Through a variety of exercises, these worksheets cater to different learning styles and interests, making the concept of patterns accessible and engaging for all students. As students become more proficient in identifying and creating AB patterns, they lay the groundwork for more advanced mathematical thinking and reasoning skills, setting the stage for academic success in the years to come.
Types of Exercises
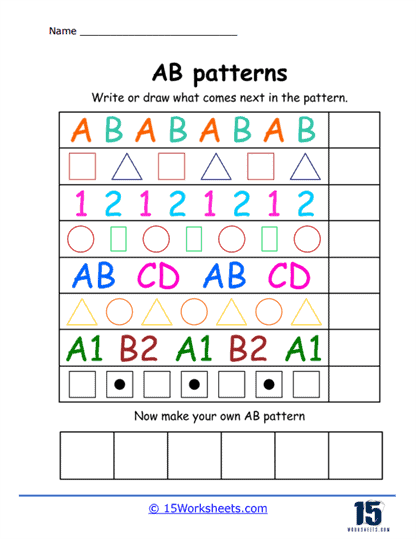
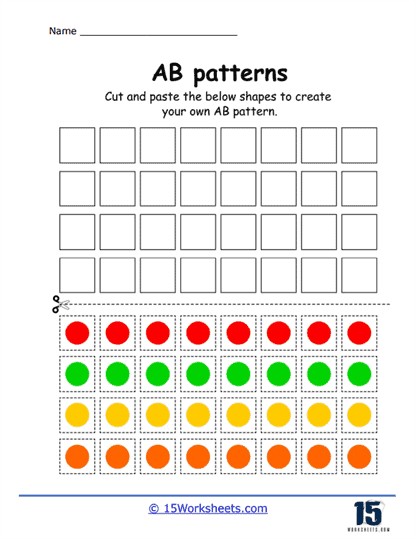
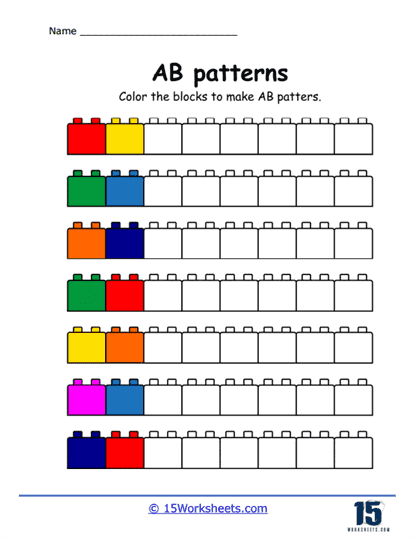
Color Patterns – These exercises require students to identify and continue a pattern using colors. For example, a worksheet might present a sequence of colors like red, blue, red, blue, and ask the student to add the next two colors in the pattern. This exercise enhances color recognition and introduces the concept of alternating patterns.
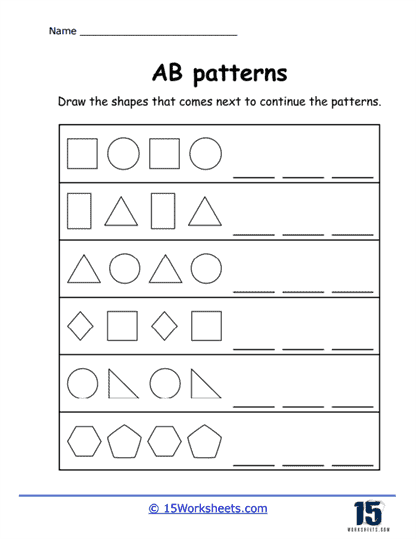
Shape and Object Patterns – Shape patterns involve sequences of different shapes. Students might be asked to determine what shape comes next in a pattern of circle, square, circle, square. This type not only reinforces the concept of AB patterns but also aids in shape identification and differentiation. Using everyday objects or thematic items, these exercises make patterns more tangible. Students might see a pattern of apple, banana, apple, banana, and need to determine what comes next. This approach can make learning more engaging and contextually relevant.
Number and Letter Patterns – Although slightly more complex, number patterns adhere to the AB sequence using numbers. For instance, a worksheet might present a sequence like 1, 2, 1, 2, and ask for the next numbers. This exercise begins to bridge the gap between pattern recognition and numeracy. Similar to number patterns, letter patterns use the alphabet to create AB sequences, such as A, B, A, B. This exercise supports both pattern recognition and literacy skills.
Creating Patterns – Beyond identifying and continuing patterns, some worksheets challenge students to create their own AB patterns using a set of given elements. This activity fosters creativity and deeper understanding of pattern structures.
Benefits of These Worksheets
Practicing with AB Patterns Worksheets offers numerous benefits in developing a child’s cognitive and academic skills:
Understanding of Patterns – These worksheets are foundational in teaching the concept of patterns, a critical mathematical concept. Understanding patterns helps students predict and understand sequences, which is essential in math, science, and everyday problem solving.
Numeracy and Number Sense – By incorporating numbers into patterns, worksheets enhance a student’s ability to count, recognize numbers, and understand basic arithmetic principles. This early numeracy is crucial for more complex mathematical reasoning and operations later on.
Problem Solving – Identifying and continuing patterns require students to think logically and predict outcomes based on given sequences. This process strengthens problem-solving skills as students must analyze information and make educated guesses. When students create their own patterns, they exercise creativity and personal expression. This aspect of pattern worksheets supports imaginative thinking and innovation, which are valuable in all fields of study and aspects of life.
Critical Thinking – AB Patterns Worksheets encourage students to apply critical thinking by asking them to identify rules within patterns and use these rules to determine what comes next. This skill is valuable across all areas of study and daily life, as it promotes reasoning and the ability to make connections. Successfully working with patterns requires a keen eye for detail. Students learn to notice subtle differences and similarities between items, a skill that enhances observational abilities and concentration.
Confidence in Learning – Mastering the concept of AB patterns can provide a confidence boost to young learners. Achieving success in these exercises can foster a positive attitude towards learning more complex mathematical concepts, reducing anxiety and building a solid foundation for future academic challenges.
How to Spot AB Patterns
Spotting an AB pattern in a sequence, especially with numbers, involves identifying a recurring sequence of two elements that alternate in a predictable manner. An AB pattern is the simplest form of a repeating pattern, where “A” and “B” represent two distinct elements that could be numbers, shapes, colors, or any other identifiable markers. This skill is fundamental in developing mathematical reasoning, as it lays the groundwork for understanding more complex patterns and sequences, vital in many areas of math and critical thinking.
In the context of numbers, these elements are numerical values that alternate in a specific, predictable order. Here’s a step-by-step guide on how to identify an AB pattern in a sequence of numbers:
Step #1. Observe the Sequence – The first step is to carefully observe the given sequence of numbers. Look for any repeating elements or groups of elements. An AB pattern will have two distinct elements repeating in the same order.
Example Sequence – 2, 5, 2, 5, 2, 5
Step #2. Identify the Elements – After observing the sequence, identify the two distinct elements or numbers that might constitute the pattern. In an AB pattern, these two elements will alternate.
Example Identification – In the sequence 2, 5, 2, 5, 2, 5, the elements are 2 (A) and 5 (B).
Step #3. Check for Regular Alternation – Verify that these elements alternate regularly throughout the sequence without any deviation. An AB pattern means the sequence will start with “A”, followed by “B”, and this two-part pattern will repeat without variation.
Example Check – In 2, 5, 2, 5, 2, 5, after 2 (A) always comes 5 (B), and this pattern repeats without interruption or variation, confirming an AB pattern.
Step #4. Predict the Next Elements – A good test to confirm you’ve correctly identified an AB pattern is to predict the next few elements in the sequence based on the pattern you’ve identified. If your prediction fits into the established sequence, you have successfully spotted the AB pattern.
Example Prediction – Given the sequence 2, 5, 2, 5, 2, 5, and identifying the pattern as AB (where A=2 and B=5), you would predict the next elements to be 2, 5 continuing the AB pattern.
Step #5. Generalize the Pattern – Understanding the AB pattern allows you to abstract and generalize the pattern beyond the given sequence. This means you can create a rule based on your observation, such as “The sequence alternates between 2 and 5.”
Example Generalization – For 2, 5, 2, 5, 2, 5, the general rule is – “Alternate between 2 and 5.”
Step #6. Apply to Varied Contexts – Once you grasp how to spot an AB pattern in a numerical sequence, you can apply this knowledge to other contexts, such as sequences of colors, shapes, letters, or any set of two alternating elements.