Surface Area of Pyramids Worksheets
About These 15 Worksheets
These worksheets will enhance student understanding of geometry, particularly the surface area of pyramids. These worksheets focus on teaching students how to calculate the total surface area of various types of pyramids by breaking down the process into manageable steps. Understanding the surface area of pyramids is crucial for solving real-world problems and has applications in various fields.
Math Skills Explored
Finding the surface area of pyramids worksheets explores several fundamental math skills, beginning with an understanding of geometric shapes and properties. Students must first recognize the components of a pyramid, including its base, triangular faces, apex, and slant height. This foundational knowledge is crucial as it allows students to visualize the three-dimensional shape and comprehend how its two-dimensional net unfolds. This exercise reinforces spatial reasoning and the ability to mentally manipulate shapes, skills essential in geometry and higher-level mathematics.
These worksheets emphasize the application of surface area formulas. To calculate the surface area of a pyramid, students need to determine the area of the base and the areas of the triangular faces. This typically involves using formulas for the area of different polygons, depending on the shape of the base (e.g., square, rectangular, or triangular). Students practice breaking down the problem into smaller, manageable parts, calculating each area separately before summing them to find the total surface area. This step-by-step approach reinforces algebraic manipulation and arithmetic skills, ensuring students can accurately perform calculations and apply formulas correctly.
The worksheets require students to solve for unknown dimensions using given information, which develops their problem-solving and algebraic skills. For instance, students might be given the total surface area and some dimensions of the pyramid, and they must work backward to find a missing length or height. This type of problem necessitates a deeper understanding of the relationships between different parts of the pyramid and encourages students to think critically and use algebraic techniques to isolate and solve for variables.
Types of Exercises
These worksheets contain a variety of problems designed to help students understand and apply the concept of surface area to pyramids. These problems are structured to gradually build up students’ skills and confidence in dealing with different aspects of the geometry of pyramids.
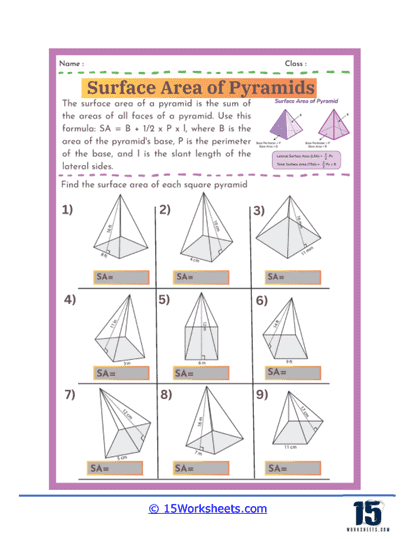
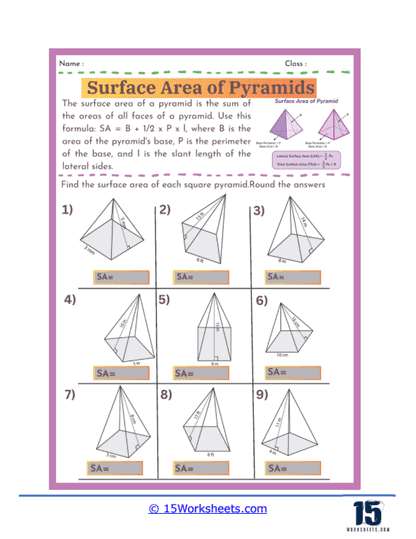
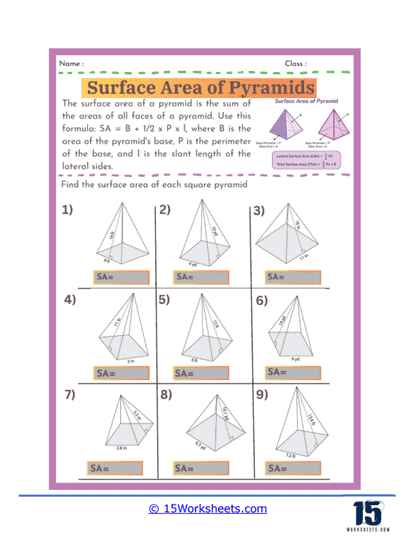
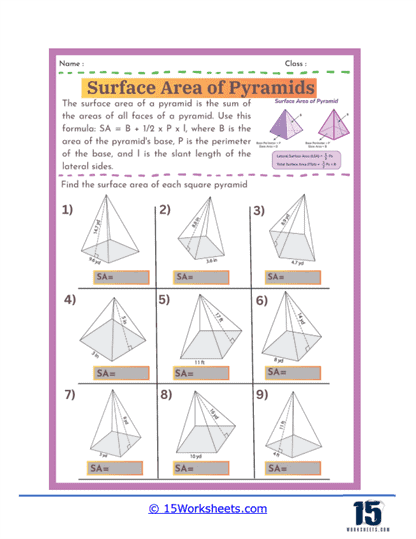
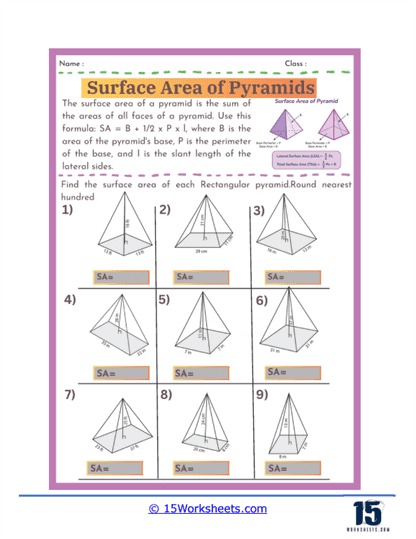
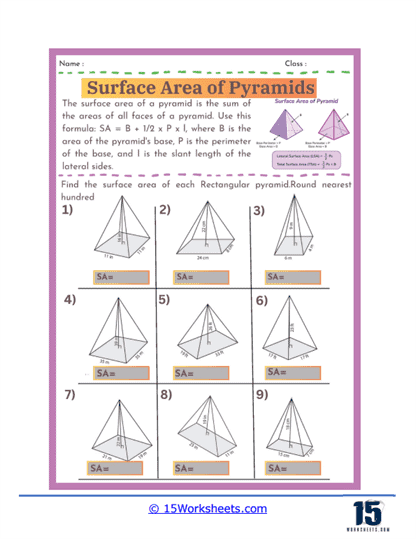
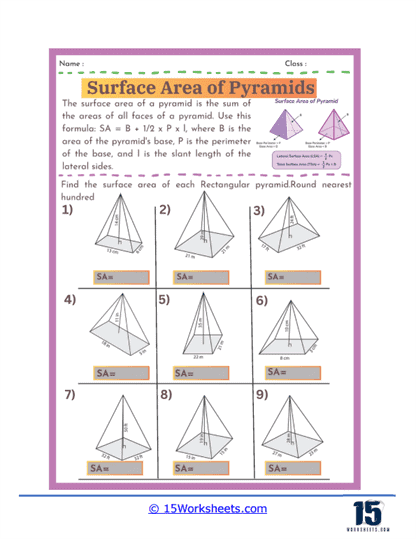
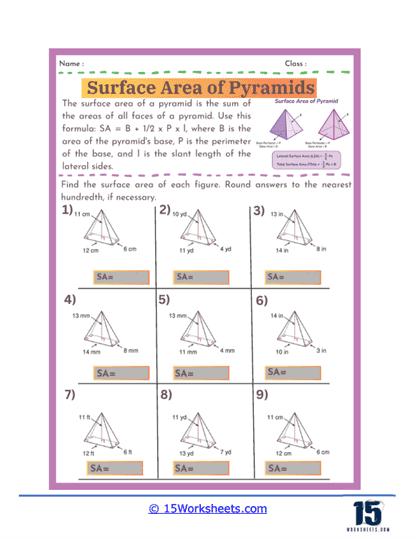
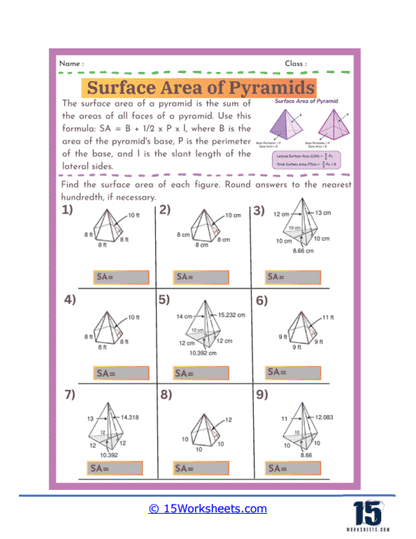
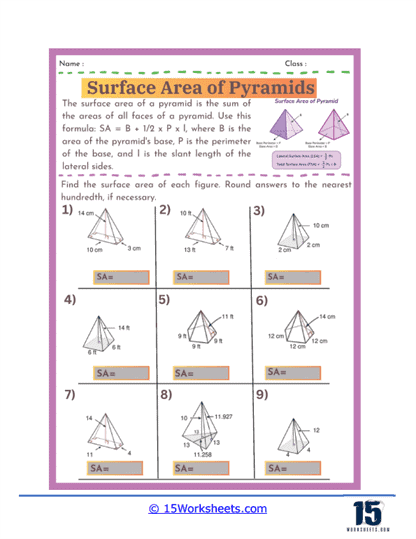
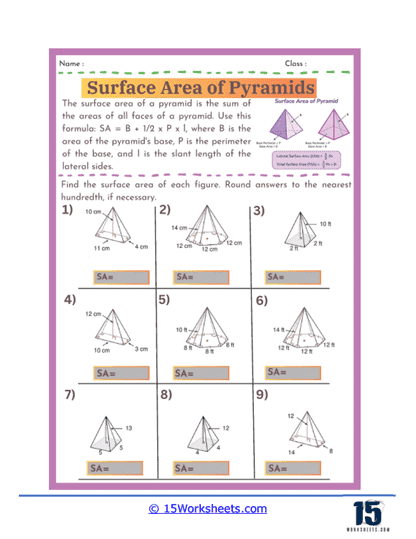
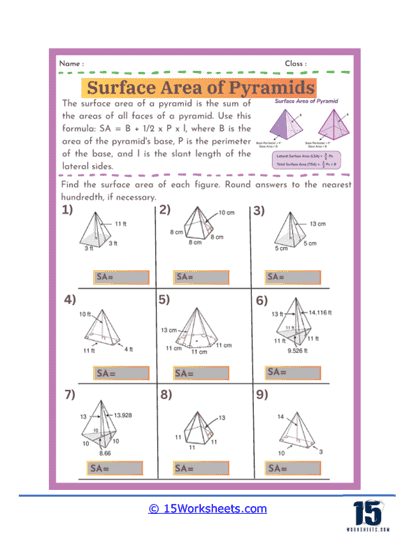
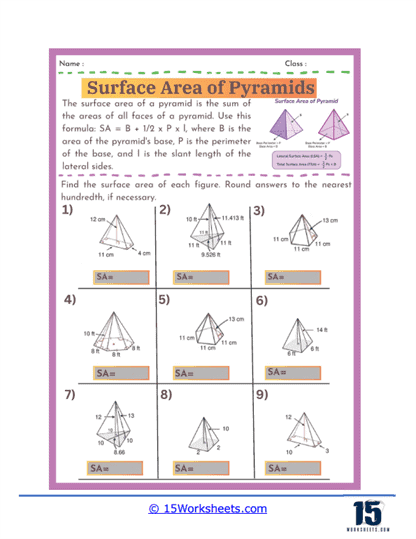
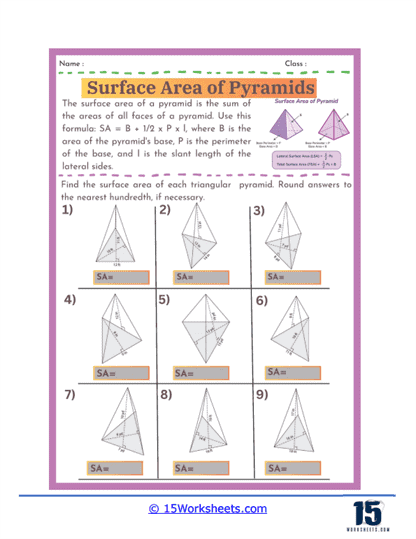
Basic Calculations – The most fundamental problems on these worksheets involve straightforward calculations where students are given the dimensions of a pyramid, such as the length of the base edges and the slant height, and asked to find the surface area. These exercises require students to apply the surface area formula for pyramids, which involves calculating the area of the base and the areas of the triangular faces, then summing these areas. For a square-based pyramid, the formula is A = B + ½ Pl, where B is the area of the base, P is the perimeter of the base, and l is the slant height.
Finding Missing Dimensions – Another common type of exercise involves problems where students must find a missing dimension given the surface area and some other measurements. For example, students might be given the total surface area and the base length and asked to solve for the slant height. These problems require students to rearrange the surface area formula and solve for the unknown variable, reinforcing their algebraic manipulation skills.
Word Problems – Many worksheets include word problems that place pyramids in real-world contexts. These scenarios might describe objects like tents, pyramidal roofs, or ancient monuments, asking students to calculate the surface area required for construction materials or painting. Such problems develop students’ ability to translate descriptive information into mathematical equations and apply geometric principles to practical situations.
Composite Figures – More advanced worksheets might include problems involving composite figures where a pyramid is combined with other shapes, such as prisms or cylinders. Students might be asked to find the total surface area of a structure that includes a pyramidal section. These exercises challenge students to break down complex shapes into simpler components, calculate the surface area of each part, and then combine these areas to find the total.
Nets and Surface Area – Some problems may involve drawing or working with nets of pyramids. Students might be asked to sketch the net of a pyramid, showing the base and the triangular faces laid out flat. They then use these nets to calculate the surface area. This type of exercise helps students develop a more intuitive understanding of how three-dimensional shapes unfold into two-dimensional representations, enhancing their spatial reasoning skills.
Optimization Problems – Advanced worksheets might include optimization problems where students are tasked with finding dimensions that maximize or minimize the surface area for a given volume. These problems integrate concepts from calculus with geometry and require students to use higher-order thinking to derive and solve equations that describe the relationships between different dimensions of the pyramid.
Benefits of Surface Area Worksheets
Learning how to calculate the surface area of pyramids offers several significant benefits, both academically and practically. First and foremost, it deepens students’ understanding of geometry by introducing them to three-dimensional shapes and their properties. The process of calculating surface areas requires students to break down complex figures into simpler components, reinforcing their spatial reasoning and ability to visualize and manipulate shapes. This foundational knowledge is crucial for advancing in mathematics, particularly in fields that involve three-dimensional modeling and design.
Mastering the calculation of surface areas enhances critical thinking and problem-solving skills. Students must interpret given dimensions, apply geometric formulas, and perform accurate calculations. This methodical approach cultivates attention to detail and logical reasoning, which are essential skills not only in mathematics but also in various academic disciplines and professional fields. By tackling these problems, students also develop perseverance and the ability to handle complex tasks, preparing them for more advanced studies and real-world challenges.
Real-World Applications
Understanding how to calculate the surface area of pyramids has practical applications across numerous fields. In architecture and construction, accurate surface area calculations are vital for determining the amount of materials needed for building projects. For example, when designing a pyramid-shaped roof or monument, knowing the surface area helps in estimating the quantity of roofing material or paint required, which directly impacts project planning and budgeting. This precision ensures efficient use of resources, reduces waste, and controls costs, which are critical factors in the construction industry.
In manufacturing, especially in industries that produce items with pyramidal shapes, calculating the surface area is essential for material optimization and quality control. For instance, manufacturers need to know the surface area to apply coatings, finishes, or protective layers evenly across a product. This ensures consistency and durability, leading to higher-quality products. Understanding surface area also aids in packaging design, where the efficient use of materials can result in cost savings and environmental benefits.
Having the ability to calculate the surface area of pyramids is useful in various scientific fields. In environmental science, for example, understanding the surface area of natural pyramidal formations can help in studying erosion patterns, water runoff, and other geological processes. This knowledge can inform conservation strategies and land management practices. Similarly, in the field of archaeology, calculating the surface area of ancient pyramidal structures aids in the preservation and restoration of these historical sites.