Surface Area of Composite Figures Worksheets
About These 15 Worksheets
These worksheets are designed to help students understand and calculate the surface area of composite shapes, which are figures made up of two or more simple geometric shapes. These worksheets guide students through the process of breaking down complex shapes into manageable parts and applying the appropriate formulas to find the total surface area. By working through these worksheets, students develop a deeper understanding of geometric principles and enhance their problem-solving skills.
Mathematical Skills Explored
One of the primary skills is spatial reasoning. Students must visualize the composite figure as a combination of simpler shapes, understand how these shapes fit together, and determine which surfaces are part of the external area. This ability to mentally deconstruct and reconstruct complex figures is crucial for accurately calculating surface areas.
Another key skill developed through these worksheets is the application of geometric formulas. Students need to recall and use the appropriate formulas for calculating the area of basic shapes such as rectangles, triangles, circles, and other polygons. This reinforces their knowledge of geometric properties and helps them understand how these properties extend to more complex shapes. Additionally, students learn to adapt these formulas to different contexts, enhancing their mathematical flexibility and problem-solving abilities.
Attention to detail and precision in calculations are also critical skills honed through these exercises. Finding the surface area of composite figures often involves multiple steps and intermediate calculations. Students must carefully keep track of each step, ensure accuracy in their measurements and calculations, and correctly sum the areas of the individual shapes. This practice helps students develop meticulousness and accuracy, which are essential qualities in all areas of mathematics and many real-world applications.
These worksheets also encourage logical reasoning and sequential thinking. To solve for the surface area of a composite figure, students must follow a logical sequence of steps: identify the individual shapes, calculate their areas, and then sum these areas to find the total surface area. This structured approach to problem-solving helps students build strong logical reasoning skills, which are valuable not only in mathematics but also in fields such as science, engineering, and computer science.
Exercises and Practice Problems
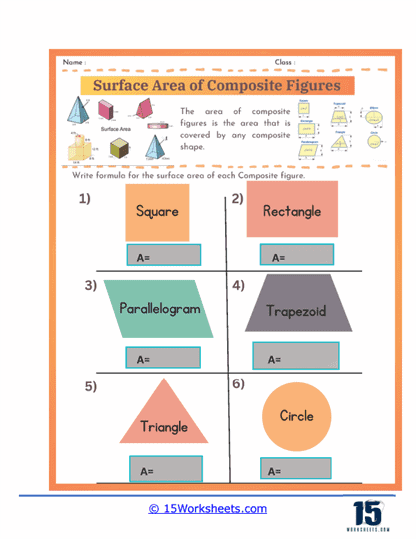
Surface area of composite figures worksheets typically include a variety of problems designed to challenge students’ understanding of how to calculate the surface area of shapes formed by combining multiple simple geometric figures, such as rectangles, triangles, circles, and polygons. These worksheets often begin with simpler problems that involve composite figures made up of just two or three basic shapes, allowing students to practice the fundamental skills of breaking down a complex shape into its simpler components, calculating the surface area of each component, and then summing these areas.
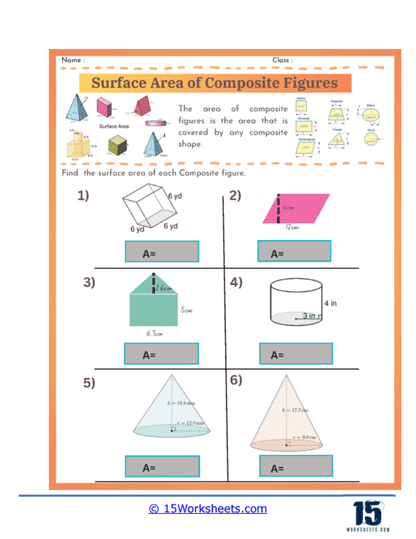
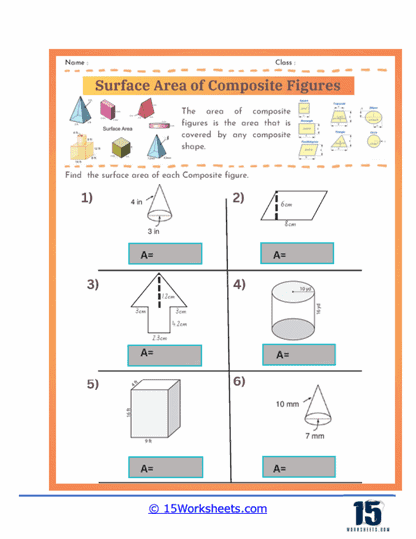
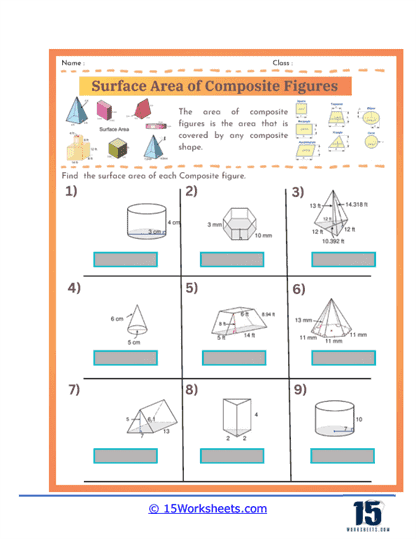
As students progress, the worksheets introduce more complex composite figures that require a higher level of spatial reasoning. These figures might include three-dimensional shapes such as prisms, cylinders, cones, and spheres combined in various ways. Problems may involve composite solids where students need to identify and calculate the surface area of visible faces, including those partially obscured or overlapping with other shapes. This helps students develop their ability to visualize and mentally manipulate three-dimensional objects.
Another common type of exercise on these worksheets involves real-world applications. These problems might ask students to calculate the surface area of composite figures that represent everyday objects, such as a house with a cylindrical tower or a storage container with multiple sections. These practical applications help students understand the relevance of surface area calculations in real life and improve their problem-solving skills by applying mathematical concepts to tangible scenarios.
To further enhance critical thinking, some worksheets may include problems that involve subtracting areas. For instance, students might be given a composite figure with a cut-out section, such as a rectangular pool with a circular hot tub area removed. These problems require students to calculate the area of the entire figure first and then subtract the area of the cut-out section, reinforcing the concept of negative space in composite figures.
Benefits of These Worksheets
Learning how to calculate the surface area of composite figures offers several educational benefits. Firstly, it enhances spatial reasoning and visualization skills, as students must break down complex shapes into simpler components, understand their individual properties, and reassemble these components mentally. This process strengthens their ability to think in three dimensions and improves their overall geometric intuition, which is fundamental in various fields of mathematics and science.
Mastering this skill fosters a deeper understanding of geometric principles and the relationships between different shapes. By calculating surface areas, students reinforce their knowledge of the properties and formulas associated with basic geometric figures like rectangles, triangles, and circles. This repetition and application of concepts to more complex problems solidify their grasp of geometry, providing a strong foundation for more advanced mathematical studies.
Learning to calculate the surface area of composite figures enhances problem-solving and critical thinking abilities. These exercises often involve multiple steps, requiring students to plan and execute a sequence of calculations accurately. This step-by-step approach promotes logical thinking and precision, skills that are valuable not only in mathematics but in a wide range of academic and professional contexts.
Uses In The Real World
In the real world, the ability to calculate the surface area of composite figures is crucial in various practical applications. In architecture and construction, for instance, determining the surface area of composite shapes is essential for tasks such as estimating the amount of materials needed for building projects, including paint, tiles, and insulation. Accurate surface area calculations help ensure that resources are appropriately allocated, reducing waste and optimizing costs.
In manufacturing, this skill is equally important. Product designers and engineers often work with complex shapes and need to calculate their surface areas to determine the amount of material required for production, the cost of materials, and the feasibility of manufacturing processes. This is particularly relevant in industries such as automotive, aerospace, and consumer goods, where precise measurements directly impact product quality and efficiency.
In environmental science and engineering, calculating the surface area of composite figures plays a role in understanding and managing various natural and man-made systems. For example, in water treatment facilities, engineers must calculate the surface area of tanks and filtration units to ensure proper flow rates and treatment efficiency. Similarly, in agriculture, determining the surface area of irregularly shaped fields is important for accurate irrigation and fertilization planning.