Surface Area of Cones Worksheets
About These 15 Worksheets
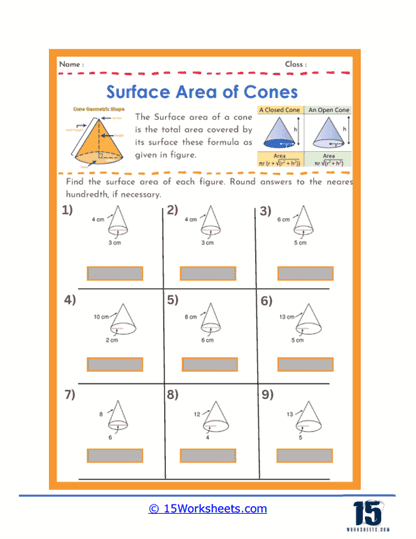
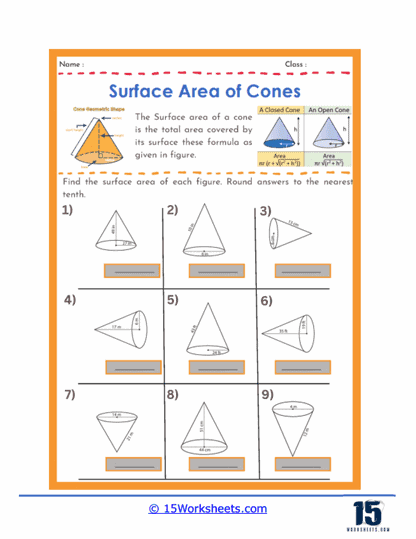
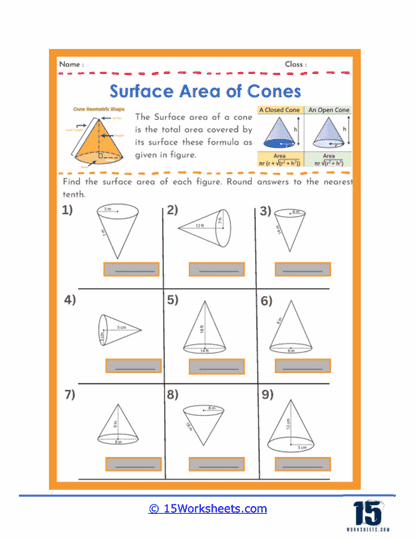
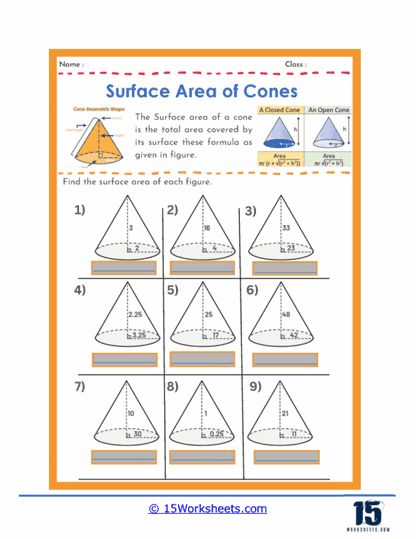
These worksheets will help students understand and calculate the surface area of conical shapes. These worksheets guide students through the steps required to determine the total area covered by the surface of a cone, using specific geometric formulas. By working through these worksheets, students develop a deeper understanding of geometric principles and improve their mathematical problem-solving skills.
Mathematical Skills Explored
Worksheets focused on finding the surface area of cones help students develop and reinforce several key math skills essential for understanding and solving these problems accurately. One of the primary skills is the application of geometric formulas. To find the surface area of a cone, students must use the formula πr(r + l), where r is the radius of the base and l is the slant height. This exercise reinforces their ability to apply specific geometric formulas and enhances their understanding of the relationship between the different dimensions of a cone.
Another critical skill developed through these worksheets is spatial reasoning. Students need to visualize the three-dimensional nature of a cone and understand how its two-dimensional base and slant height combine to form its surface area. This visualization helps students grasp the concept of surface area as the sum of the areas of the base and the curved surface, improving their ability to think about and manipulate three-dimensional objects.
Attention to detail and precision in measurement and calculation are also emphasized in these exercises. Calculating the surface area of a cone requires accurate measurement of the radius and slant height, as well as precise computation using the formula. This practice helps students develop meticulousness and accuracy, which are essential skills in all areas of mathematics and many real-world applications.
Logical reasoning and sequential thinking are further strengthened as students follow a clear sequence of steps to solve these problems. They must first measure the relevant dimensions, then apply the formula to calculate the surface area. This structured approach to problem-solving helps students build strong logical reasoning skills, which are valuable not only in mathematics but also in fields such as science, engineering, and technology.
Exercises on These Worksheets
Surface area of cones worksheets typically contain a variety of problems that help students understand and apply the formula for calculating the surface area of cones. The types of problems and exercises on these worksheets are designed to reinforce the concepts of geometry, specifically focusing on the properties of cones and their surface areas.
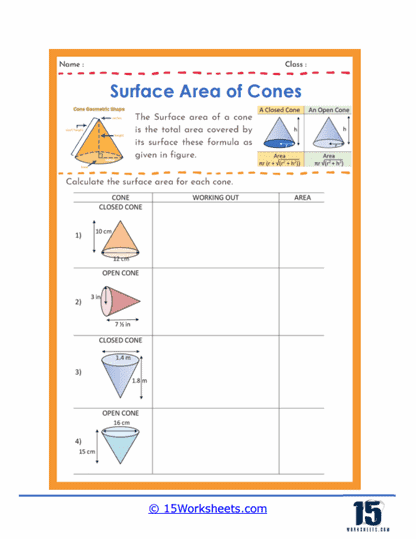
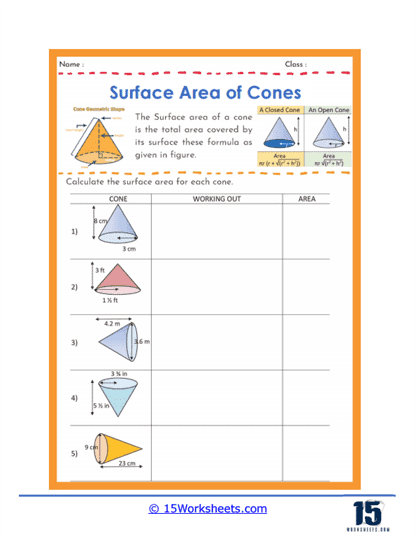
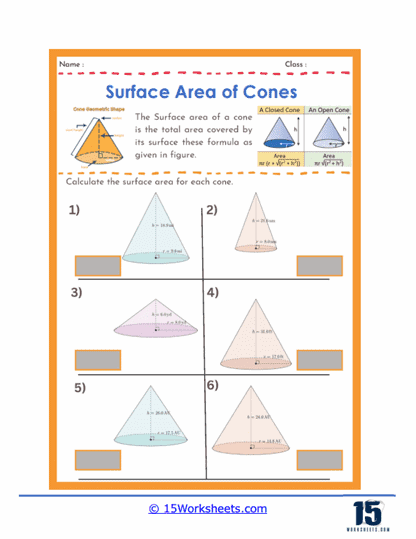
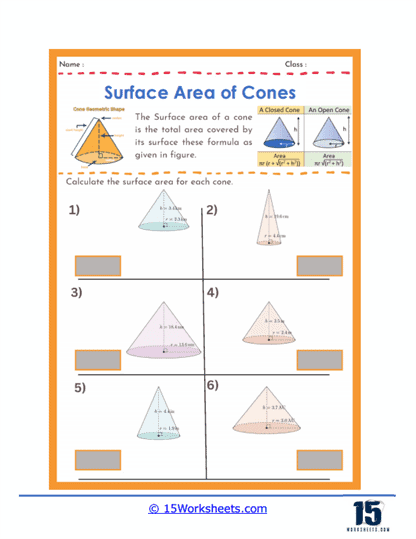
Basic Calculations – One of the most common types of problems involves straightforward calculations where students are given the radius and the slant height of a cone and are asked to find its surface area. These problems help students practice the formula for the surface area of a cone, which is the sum of the base area and the lateral surface area, represented by A = πr(r + l), where r is the radius and l is the slant height.
Finding Missing Dimensions – Another typical exercise involves problems where students need to find a missing dimension given the surface area and one other dimension (either the radius or the slant height). For example, students might be given the surface area and the radius and asked to solve for the slant height. These types of problems require students to manipulate the surface area formula algebraically, enhancing their algebra skills alongside their understanding of geometry.
Word Problems – Worksheets often include word problems that require students to apply their knowledge in real-world contexts. These problems might describe a scenario, such as designing a conical tent or a lampshade, and ask students to calculate the surface area needed for materials. These exercises develop students’ ability to translate textual information into mathematical problems and apply geometric concepts to practical situations.
Composite Figures – Some advanced worksheets may include problems involving composite figures where the cone is combined with other shapes, such as cylinders or spheres. Students might be asked to calculate the total surface area of a structure that includes a conical section. These problems require a deeper understanding of how to break down complex figures into simpler parts and apply the surface area formulas accordingly.
Problem Solving with Nets – Another type of exercise involves working with nets of cones. Students may be asked to draw the net of a cone, which includes a circular base and a sector of a circle for the lateral surface. They then use these nets to visualize and calculate the surface area. This type of exercise helps students develop spatial reasoning skills and understand the geometric properties of cones more concretely.
Benefits of These Worksheets
Learning how to calculate the surface area of cones offers numerous benefits for students, both in terms of academic development and practical application. Firstly, mastering this skill strengthens students’ understanding of geometry, particularly in the area of three-dimensional shapes. Calculating the surface area of cones requires familiarity with geometric formulas, the ability to manipulate algebraic expressions, and spatial reasoning. This foundational knowledge is critical for advancing in mathematics, as it underpins more complex concepts and problem-solving techniques.
The process of learning to calculate surface areas enhances critical thinking and analytical skills. Students must interpret the given information, apply the correct formulas, and accurately perform calculations. This step-by-step problem-solving approach fosters attention to detail and logical reasoning, skills that are valuable not only in mathematics but also in various academic and professional fields. Additionally, students develop perseverance and the ability to tackle challenging problems, which are essential traits for success in any discipline.
Real World Applications
The ability to calculate the surface area of cones also has significant real-world applications. For instance, in engineering and architecture, understanding the surface area is crucial when designing conical structures such as roofs, towers, and chimneys. Accurate calculations ensure that the correct amount of materials is used, preventing wastage and reducing costs. This knowledge is particularly important in the construction industry, where precise measurements directly impact the quality and efficiency of a project.
In manufacturing, especially in industries that produce conical objects like funnels, pipes, and storage tanks, calculating the surface area is vital for determining material requirements and production costs. For example, manufacturers need to know the surface area to apply coatings, paints, or other finishes to their products. This ensures uniform application and quality control, leading to better product durability and aesthetics.
The skill is beneficial in everyday life and various other professions. In culinary arts, chefs and bakers often need to calculate the surface area of conical molds to determine the amount of ingredients required for recipes. Similarly, in environmental science, understanding the surface area of conical landforms can be important for studying erosion patterns and designing conservation strategies.