Properties of Division Worksheets
About These 15 Worksheets
These worksheets focus on developing an understanding of division as an operation and the specific characteristics or “properties” that are consistent no matter which numbers are being divided. As a core math skill, division can be tricky for students, so breaking it down into various properties allows for easier comprehension. Properties of Division worksheets offer students repeated practice with key rules that simplify division, while also reinforcing related mathematical operations like multiplication and subtraction. Let’s walk through the different types of tasks you might expect to find on these worksheets, along with the skills they help to build.
Understanding Division by 1
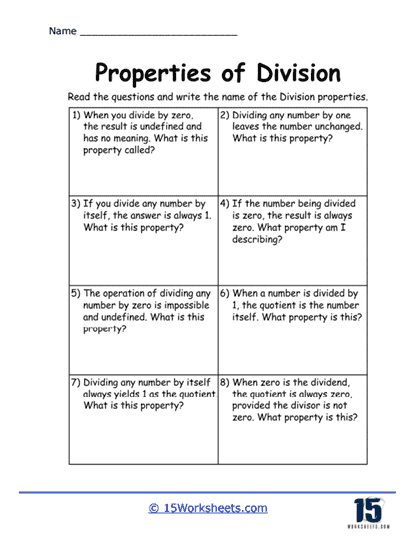
One of the most common properties of division is the rule that any number divided by 1 remains unchanged. This is a critical first step in learning division because it shows students that dividing by 1 doesn’t alter the value of the number. On a typical Properties of Division worksheet, you’d find a series of problems like 45 ÷ 1 = or 98 ÷ 1 =, where students quickly learn that dividing by 1 leaves the number exactly as it is. This basic principle reinforces the idea of identity in division and helps lay the foundation for understanding more complex division problems. It also builds confidence, as students are able to recognize patterns and apply this rule across all kinds of numbers.
Understanding Division by Itself
Another fundamental property that often shows up in these worksheets is the concept that any number divided by itself equals 1. Worksheets usually include exercises like 12 ÷ 12 = or 64 ÷ 64 =, giving students plenty of practice with this important rule. This concept solidifies the relationship between division and equality, reinforcing the idea that when you divide a whole by itself, you’re left with a single unit. This is essential for students’ broader understanding of fractions and ratios, as they begin to conceptualize how parts and wholes relate to each other.
Division by Zero
A more complex property involves the rule that dividing any number by zero is undefined. This can be confusing at first, but it’s crucial for students to understand that division by zero doesn’t work because there’s no way to split something into zero parts. On a Properties of Division worksheet, you’d likely see a mix of division problems, including some that divide by zero, such as 15 ÷ 0 =, and students must write “undefined” or “no solution.” These exercises teach students that, unlike multiplication or addition, division has restrictions on when it can be used. It also encourages critical thinking, as students have to identify when the operation they’re attempting isn’t possible.
The Relationship Between Operations
Another key feature you’ll find on these worksheets is exercises that demonstrate the inverse relationship between multiplication and division. For example, problems might ask students to use multiplication to check their division, like solving 24 ÷ 8 = and then verifying it by multiplying 3 x 8 to check that it equals 24. This relationship is fundamental because it shows students how division is simply the reverse of multiplication. On more advanced worksheets, students might encounter fact families, where they’re given a set of related multiplication and division problems. For instance, if they know that 5 x 6 = 30, they should also be able to conclude that 30 ÷ 5 = 6 and 30 ÷ 6 = 5. Fact families help students see the interconnectedness of math operations and develop fluency with both division and multiplication facts.
Dividing Larger Numbers and Long Division
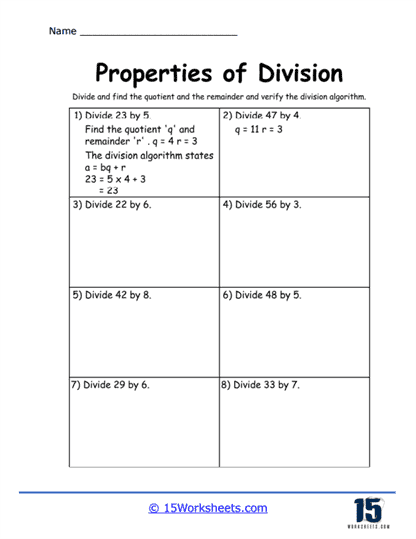
As students become more proficient in their division skills, Properties of Division worksheets often introduce problems involving larger numbers or long division. These exercises challenge students to apply the basic division properties they’ve learned to more complex problems. Worksheets may feature problems like 4,968 ÷ 12 =, where students need to use long division to arrive at the correct answer. Along with basic division facts, these worksheets help students develop their procedural skills in long division, which is a more methodical approach that involves multiple steps: dividing, multiplying, subtracting, and bringing down the next digit.
Long division is an essential skill because it enables students to tackle problems involving larger numbers, which they’ll encounter often in higher-level math. It also helps students work on their organizational skills and attention to detail, as long division requires them to follow a specific sequence of steps to get the correct answer. As students progress, these worksheets may also introduce problems with remainders, like 53 ÷ 4 = 13 R1, helping students to understand that division doesn’t always result in a neat, whole number.
Estimation in Division
Estimation is another critical skill developed through Properties of Division worksheets. When dividing larger numbers, students often need to make estimates to determine how many times a divisor can fit into the dividend. For example, in the problem 375 ÷ 12, students might start by estimating that 12 goes into 37 about 3 times, and then work from there. Estimation helps students become more comfortable with approximate answers, which is a valuable skill in real-world math scenarios, like budgeting or measuring. Worksheets may include estimation exercises that ask students to round both the dividend and divisor to the nearest ten and then solve, such as 625 ÷ 24 ≈ 600 ÷ 20.
Divisibility Rules
A particularly engaging type of exercise you’ll often find in Properties of Division worksheets involves practicing divisibility rules. These are shortcuts that help students quickly determine whether a number can be divided by another without actually performing the division. For example, a worksheet might ask students to circle all numbers divisible by 3 or 5 in a given set. Divisibility rules, such as “a number is divisible by 3 if the sum of its digits is divisible by 3,” give students quick strategies to check division problems mentally. This helps improve their number sense and enables them to spot patterns and relationships between numbers. Mastery of divisibility rules is essential as students begin working with fractions, factors, and multiples.
From basic concepts like dividing by 1 or by itself, to understanding the relationship between multiplication and division, and even tackling long division and word problems, these worksheets provide comprehensive practice. They help build the critical skills students need to master division and prepare them for more advanced mathematical challenges.