Multiplication As Repeated Addition Worksheets
About These 15 Worksheets
Teaching multiplication as an extension of addition is an invaluable strategy, especially for young learners beginning their mathematical journey. The worksheets that use this approach offer students a clear, hands-on understanding of how these two operations are linked. Rather than diving headfirst into multiplication, which can seem abstract and intimidating, these resources gently guide students by first reinforcing the familiar concept of addition. By doing so, they allow students to grasp multiplication as a simple process of grouping and adding repeatedly. This initial connection between addition and multiplication lays a foundation for more complex mathematical concepts, turning multiplication from an abstract idea into something tangible and approachable.
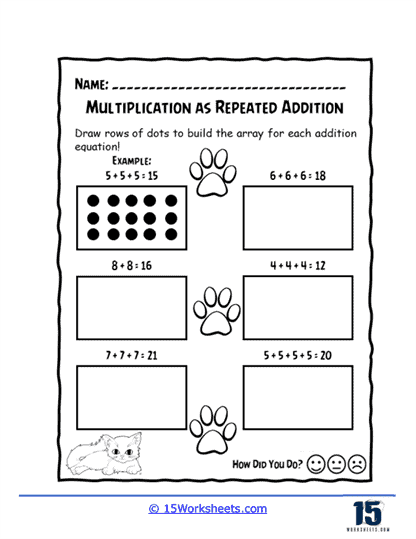
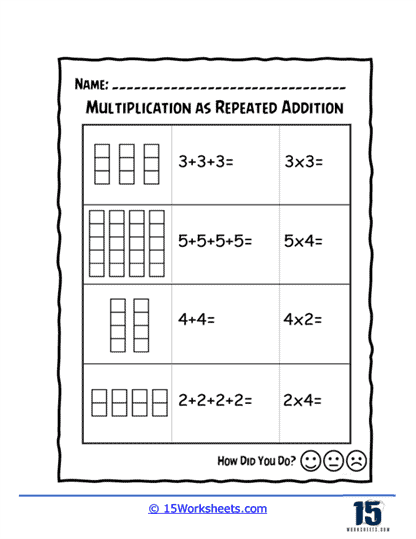
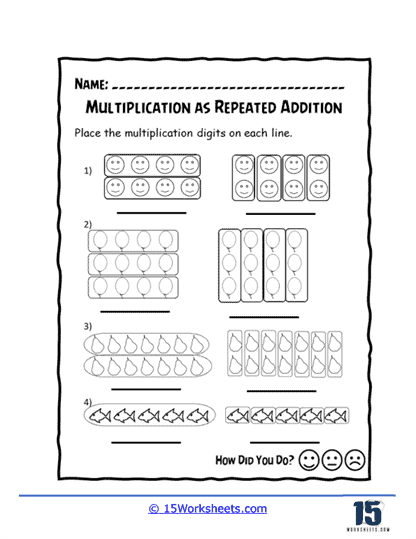
One of the primary benefits of these worksheets is their focus on repeated addition. For example, when a student is asked to add 4 + 4 + 4, they are not just performing a basic arithmetic task but are also taking the first steps towards understanding that multiplication can replace this repetitive addition. The transition from writing out multiple additions to a simple multiplication equation like 3 × 4 becomes natural. This step-by-step method transforms multiplication into something students can visualize, reducing the cognitive load that might come with introducing both operations simultaneously. These worksheets make it easier for students to see that multiplying numbers is simply grouping the same number multiple times.
The power of visualization cannot be overstated when it comes to teaching young learners. Through the use of arrays, these worksheets offer a visual representation of multiplication problems. Arrays, which organize items into rows and columns, enable students to see multiplication in a physical and concrete way. For instance, an array showing three rows of five dots not only helps students count the total number of dots (15) but also demonstrates the multiplication equation 3 × 5 in a visual format. This method is especially beneficial for students who may struggle with abstract thinking, providing a bridge between visual learning and numerical computation. By physically seeing the equal-sized groups laid out, students gain a deeper, more intuitive understanding of what multiplication represents.
These worksheets are designed with thoughtful progression, allowing students to build confidence through repetition and increasing complexity. Starting with smaller, manageable numbers, the worksheets help students become comfortable with basic multiplication facts before advancing to more complex numbers and multi-step problems. This scaffolding approach ensures that learners are not overwhelmed and are able to build on their successes as they tackle more challenging tasks. As students move through these worksheets, they develop fluency with multiplication facts, solidifying their understanding and speed in recognizing and calculating basic multiplication equations.
Repetition, while sometimes seen as monotonous, plays a critical role in mastering multiplication. The worksheets often include exercises that require students to practice the same fact in different ways-whether it’s filling in blanks, matching repeated addition sentences to their corresponding multiplication equations, or interpreting arrays. This consistent, varied practice is essential for internalizing multiplication facts, helping students commit them to memory. Once these facts are committed to memory, students can recall them with ease, which is an essential skill for more advanced mathematical operations in the future, such as division, fractions, and even algebraic thinking.
But these worksheets go beyond rote memorization. They also encourage the development of critical thinking skills by presenting multiplication in real-world contexts. For instance, problems might ask students to apply multiplication to everyday scenarios like counting groups of items in a grocery store, arranging desks in a classroom, or organizing teams for a game. This practical application allows students to see the relevance of multiplication in their daily lives, reinforcing why learning this skill is important. When students can connect what they are learning to the real world, their engagement and understanding deepen. They start to see multiplication not just as a classroom exercise, but as a tool they will use outside of school.
These worksheets are designed to help students develop a flexible approach to solving problems. While some exercises may have students directly calculating multiplication facts, others might ask them to interpret arrays, create equal groups, or use different methods to reach a solution. This variety in problem-solving approaches not only strengthens their grasp of multiplication but also fosters adaptability. Students begin to understand that there are multiple ways to approach a problem, which is an essential skill in mathematics and beyond. This critical thinking component helps students move from simply following a set of rules to truly understanding the underlying concepts.
The beauty of teaching multiplication through repeated addition lies in its ability to demystify an otherwise abstract concept. When students first encounter multiplication, they might view it as an entirely new operation. However, by framing it as nothing more than an extension of addition—something they are already familiar with—these worksheets make multiplication accessible and approachable. The visual and conceptual strategies presented in the worksheets enable students to transition smoothly from simple arithmetic to more complex mathematical thinking without feeling overwhelmed or discouraged.
In many ways, solving these multiplication worksheets is like embarking on a math adventure. Each problem is a puzzle waiting to be solved, and with every completed exercise, students are uncovering the deeper structure of numbers. As they solve these problems, they become math explorers, discovering the patterns and relationships that define how numbers work together. This sense of exploration and discovery keeps students engaged, transforming what could be a mundane task into an exciting challenge. The journey from repeated addition to mastering multiplication is one filled with small victories that lead to a greater understanding of mathematics as a whole.
These worksheets serve not just as a tool for teaching multiplication but also as a key to unlocking students’ potential in math. By helping them understand multiplication in a concrete, visual way, these resources lay the groundwork for success in future mathematical endeavors. Whether it’s learning to divide, solving algebraic equations, or tackling real-world problems, the skills students gain from these worksheets will continue to serve them. So, as they pick up their pencils and dive into these worksheets, they are not just practicing multiplication-they are setting out on a path to becoming confident, capable math learners.
How Multiplication Relates to Addition
Multiplication is fundamentally based on the concept of repeated addition. When we multiply two numbers, we are essentially adding one of the numbers repeatedly, as many times as the value of the other number dictates. This view of multiplication allows us to understand it in terms of simpler arithmetic operations and builds on a foundational understanding of addition.
For example, consider the multiplication problem 3 x 4. This can be understood as adding the number 3 repeatedly, four times:
3 + 3 + 3 + 3 = 12
Here, the number 3 is added four times, resulting in the same total as 3 x 4, which is 12. In this case, the first number (3) is the repeated element, while the second number (4) tells us how many times to repeat the addition.
Another example is 5 x 6. If we think of this in terms of repeated addition, it means adding 5 a total of six times:
5 + 5 + 5 + 5 + 5 + 5 = 30
This shows that the multiplication of 5 and 6 results in the same total as adding 5 six times, giving us the value 30.
This method works for larger numbers as well. Take 8 x 7, for instance. Using repeated addition, we add 8 seven times:
8 + 8 + 8 + 8 + 8 + 8 + 8 = 56
Thus, multiplication simplifies the process of repeated addition by providing a faster and more efficient way to arrive at the same result.
It is important to note that multiplication is commutative, meaning that the order of the numbers does not affect the product. For instance, 4 x 3 gives the same result as 3 x 4. In terms of repeated addition, we can either add 3 four times or add 4 three times:
4 + 4 + 4 = 12 or 3 + 3 + 3 + 3 = 12
Both approaches lead to the same outcome, demonstrating that multiplication is simply another way of organizing repeated addition.
Understanding multiplication in terms of repeated addition not only helps clarify the mechanics of the operation but also lays the groundwork for more advanced concepts like multiplication involving larger numbers, fractions, or variables. This perspective is a fundamental stepping stone in early mathematics education.