Equivalent Ratios Worksheets
All About These 15 Worksheets
Equivalent ratios worksheets were created to help students understand the concept of ratios and how they can be applied in various contexts. These worksheets are designed to engage students with problems that involve comparing quantities and identifying relationships between different values. At the heart of these worksheets is the concept of ratio equivalence, where students learn that two ratios can represent the same relationship even though the actual numbers involved may differ. For example, the ratio 2:3 is equivalent to 4:6 because both represent the same proportional relationship between the numbers involved.
Types of Exercises
There are several types of problems and exercises that typically appear on equivalent ratios worksheets. These exercises are designed to build a deep understanding of how ratios work, how to manipulate them, and how to apply them to real-world scenarios.
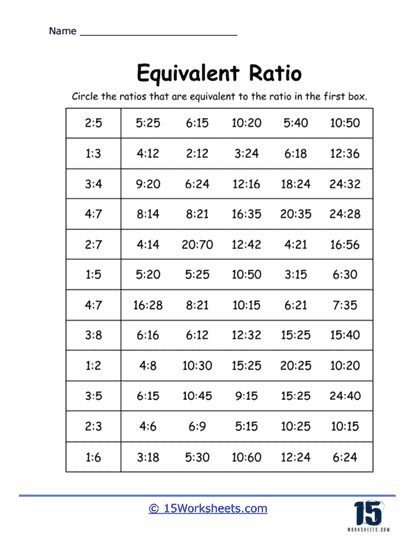
1. Basic Equivalent Ratio Problems
The most fundamental type of problem you would encounter on an equivalent ratios worksheet involves finding missing values to complete a set of equivalent ratios. For instance, students may be given a ratio like 3:5 and asked to complete another equivalent ratio, such as 6:____, where they need to figure out the corresponding second term that maintains the equivalence. This helps students learn the process of multiplying or dividing both terms of a ratio by the same number to create equivalent ratios.
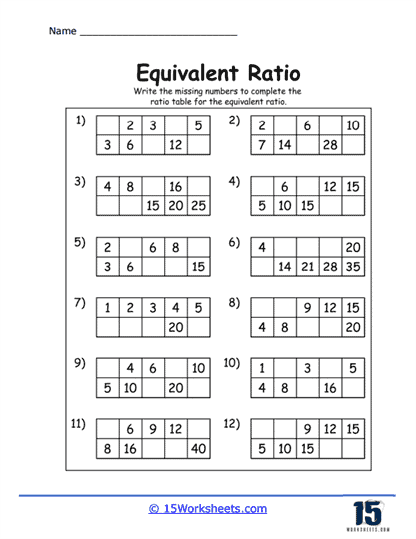
2. Ratio Tables
Another common feature of equivalent ratios worksheets is the use of ratio tables. In these tables, students are presented with one or more ratios and asked to fill in the missing entries. For example, a table may begin with the ratio 2:3, and students would need to complete rows that maintain the same ratio, such as 4:6, 6:9, and 8:12. Ratio tables are particularly useful for helping students visualize how ratios grow and shrink while maintaining their proportional relationship.
3. Word Problems
Many equivalent ratios worksheets include word problems that require students to apply their understanding of ratios in real-world situations. These problems might involve scenarios like cooking recipes, where a ratio of ingredients must be scaled up or down, or speed and distance problems, where students are asked to calculate equivalent ratios of time and distance traveled. These word problems are essential because they help bridge the gap between abstract mathematical concepts and practical, everyday applications.
4. Proportional Relationships
Some worksheets may focus on helping students identify proportional relationships between quantities. These exercises might present graphs, tables, or other data sets where students need to recognize whether the relationship is proportional and, if so, determine the constant of proportionality. For example, if students are presented with a table of distances and times for a moving object, they may be asked to determine whether the object is moving at a constant speed (i.e., whether the ratio of distance to time is constant) and then calculate equivalent ratios to predict future distances.
5. Scaling Ratios
In this type of problem, students are tasked with scaling a given ratio either up or down. For example, they might be given the ratio 5:7 and asked to scale it up by a factor of 2 or scale it down by a factor of 3. These exercises reinforce the idea that ratios are flexible and can be adjusted to fit different situations while maintaining their proportional relationship. This is particularly useful in real-world applications such as map reading, where students must understand that different scales represent the same geographic distances in different ratios.
6. Cross-Multiplication and Solving for Variables
Equivalent ratios worksheets often introduce students to the technique of cross-multiplication, which is a key strategy for solving problems involving proportions. In these exercises, students are typically presented with two equivalent ratios in the form of fractions, such as 3/4 = x/8, and asked to solve for the missing variable. Cross-multiplication helps students understand the algebraic relationship between ratios and prepares them for more advanced math topics, such as solving equations.
7. Graphing Equivalent Ratios
Some worksheets incorporate graphing exercises, where students plot points on a coordinate plane that represent different equivalent ratios. For instance, if students are working with the ratio 2:3, they might be asked to plot the points (2, 3), (4, 6), and (6, 9) on a graph. This activity helps students visualize the linear relationship between equivalent ratios and reinforces the idea that all points on the line represent the same proportional relationship. Graphing is particularly useful in geometry, as it introduces students to the concept of slope and linear equations.
8. Converting Ratios to Fractions, Decimals, and Percentages
Equivalent ratios worksheets often include exercises that require students to convert ratios into different forms, such as fractions, decimals, and percentages. For example, the ratio 3:4 can be expressed as the fraction 3/4, the decimal 0.75, or 75%. These types of problems help students see the connections between ratios and other mathematical concepts, broadening their understanding of proportional reasoning across different formats.
Practicing with equivalent ratios worksheets offers students significant benefits beyond mere numerical fluency; it also lays a strong foundation for understanding geometry and its applications in the real world. Ratios play a crucial role in many aspects of geometry, including the study of shapes, sizes, and spatial relationships.
What Makes Ratios Equivalent?
Two ratios are considered equivalent if they express the same proportional relationship between quantities, even though the actual numbers might be different. For instance, the ratios 4:2 and 6:3 are equivalent because the relationship between the two numbers in each ratio is the same. To see this, we can simplify both ratios by dividing both terms by their greatest common divisor. For 4:2, dividing both 4 and 2 by 2 gives 2:1. Similarly, dividing 6 and 3 by 3 also gives 2:1. Since both ratios simplify to the same ratio, 2:1, they are equivalent.
Another way to check if two ratios are equivalent is by cross-multiplying. If you have two ratios, a/b and c/d, and the products of the cross-multiplications are equal, that is, if a x d = b x c, then the ratios are equivalent.
Scaling Ratios Up or Down
One of the key features of equivalent ratios is that they can be scaled up or down by multiplying or dividing both terms of the ratio by the same non-zero number. This operation does not change the proportional relationship between the quantities. For example, starting with the ratio 2:3, you can multiply both terms by 2 to get 4:6, or by 3 to get 6:9. Both 4:6 and 6:9 are equivalent to 2:3 because they describe the same relationship between the two quantities.
This principle of scaling ratios is widely used in problems involving scaling models, maps, or recipes. Suppose you are building a model car at a scale of 1:10, meaning every 1 unit on the model represents 10 units on the real car. If the model car is 5 inches long, the real car would be 50 inches long because the ratio of lengths, 1:10, has been scaled up by multiplying both terms by 5.
Applications of Equivalent Ratios in Everyday Life
Equivalent ratios have many practical applications in everyday life. For example, when cooking, if a recipe calls for a ratio of 2 cups of flour to 1 cup of sugar, and you want to make a larger batch, you can scale the ratio. If you double the quantities, you’ll need 4 cups of flour and 2 cups of sugar, keeping the ratio the same. Similarly, when working with currency exchange rates, if $1 equals 0.85 euros, the ratio of dollars to euros is 1:0.85. If you exchange $10, you would get 8.5 euros, maintaining the equivalent ratio.
In the field of business, ratios like profit margins and cost-to-revenue ratios help in making financial decisions. Equivalent ratios in these contexts allow businesses to maintain consistent financial relationships as they grow in size. Similarly, in physics, ratios like speed (distance over time) can help predict how long it will take to travel different distances at the same rate of speed.