Ratios Worksheets
All About These 15 Worksheets
Introducing our comprehensive collection of ratio worksheets, designed to captivate students and deepen their understanding of essential mathematical concepts such as ratios, proportions, and their applications. These worksheets are more than just practice tools; they are structured learning experiences crafted to enhance foundational math skills that will support algebraic thinking and problem-solving later in their academic journey. Ideal for classroom use, homeschooling, or supplemental practice, these resources cater to students in upper elementary and middle school levels, providing a variety of engaging activities to strengthen their mastery of ratios, a crucial stepping stone in mathematics.
The beauty of this collection lies in its versatility and accessibility. Each worksheet is provided in an easy-to-use, downloadable PDF format, making it convenient for teachers, parents, and students to access and use them at any time. Whether they are used for quick in-class practice, targeted homework assignments, or additional review sessions, these worksheets are flexible enough to adapt to the diverse needs of learners. They also encourage independent learning, as students can work through problems at their own pace while receiving immediate feedback from the clear, step-by-step solutions provided.
One of the standout features of this collection is the incorporation of visual learning techniques, such as Bar Models. These activities ask students to draw bar diagrams to visually represent the relationship between different sets of items, making abstract concepts like ratios more concrete and understandable. For instance, students might be asked to solve a problem like, “The ratio of red balls to blue balls is 3:2. If there are 12 red balls, how many blue balls are there?” Through the bar model, students can break down the problem, step by step, and visualize the proportional relationships at play. This not only builds their confidence in solving ratio problems but also caters to learners who thrive with visual aids.
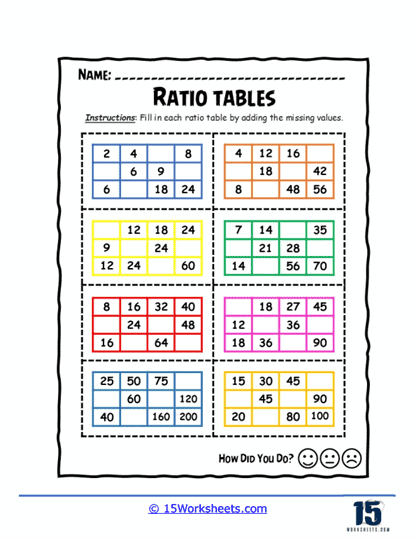
Another key component of this collection is the Ratio Tables worksheet, where students practice completing tables to find equivalent ratios. By filling in missing values and scaling ratios up or down, students hone their skills in proportional reasoning-a skill that is critical for tackling more advanced math problems like those found in algebra and geometry. These worksheets go beyond simple rote learning; they challenge students to think critically about how numbers relate to each other, preparing them to solve real-world problems such as calculating unit rates (e.g., cost per item) or determining rates of change (e.g., speed per hour). Through engaging and thought-provoking exercises, these worksheets aim to build a solid foundation that will support students throughout their mathematical education and beyond.
Categories
Here are all the different types of ratio worksheets that we have available for you:
Bar Models
These are visual tools that use rectangular bars to represent numerical relationships, helping students break down and solve word problems. They develop skills in addition, subtraction, multiplication, division, and understanding fractions, ratios, and algebraic concepts.
Equivalent Ratios
These worksheets help students practice finding and comparing ratios that have the same value by using multiplication or division. They focus on building proportional reasoning skills, essential for understanding fractions, scaling, and solving real-world problems involving ratios.
Finding The Parts From The Whole
These worksheets guide students in calculating individual parts when given the total, often using fractions, percentages, or ratios. They help develop skills in proportional reasoning, division, and fraction-to-decimal conversions, crucial for solving problems involving portions of a whole.
Part To Whole Ratio
These worksheets focus on comparing a part to the whole using ratios, helping students understand the relationship between individual quantities and their total. They develop skills in ratio comprehension, proportional reasoning, and connecting ratios to fractions and percentages.
Proportions
These worksheets help students solve problems where two ratios are set equal to each other, reinforcing the concept of equivalent ratios. They focus on developing skills in cross-multiplication, scaling, and applying proportional reasoning to real-world contexts.
Ratio Tables
These worksheets use tables to organize and compare equivalent ratios, helping students see patterns in proportional relationships. They build skills in multiplication, division, and scaling, essential for understanding ratios and solving proportion problems.
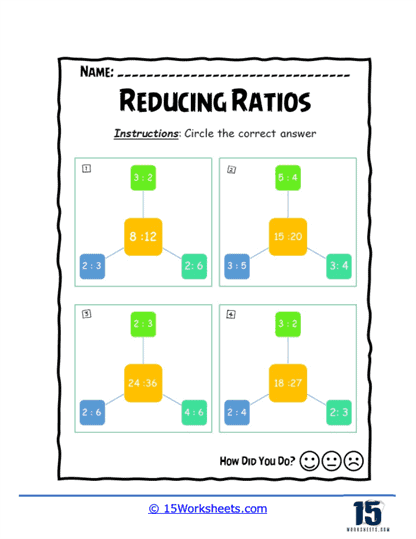
Reducing Ratios To The Lowest Terms
These worksheets teach students how to simplify ratios by dividing both terms by their greatest common factor. They develop skills in finding common factors, simplifying numerical expressions, and understanding the concept of equivalent ratios.
Scale Drawings
These worksheets involve interpreting and creating drawings where objects are represented proportionally to their actual size using a specific scale. They enhance skills in scaling, measurement, ratio reasoning, and applying proportions to real-life scenarios like maps and architectural plans.
Unit Rates
These worksheets focus on calculating the rate for a single unit, helping students understand how to compare quantities like speed, cost, or density. They strengthen skills in division, proportional reasoning, and applying rates to solve practical problems.
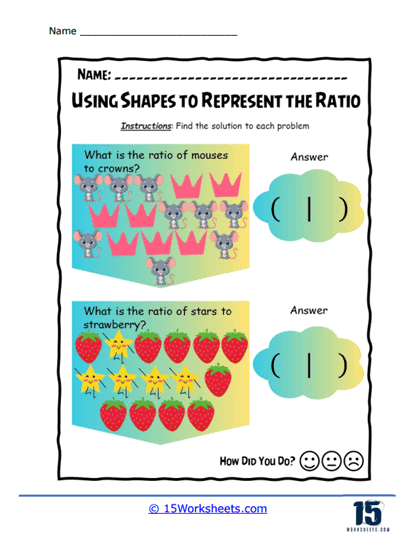
Using Shapes And Objects To Represent The Ratio
These worksheets use shapes and objects to visually represent ratios, allowing students to see the relationships between quantities. They develop spatial reasoning, proportional thinking, and the ability to translate visual models into numerical ratios.
Writing Ratios
These worksheets teach students how to express relationships between quantities in ratio form, using both words and numbers. They develop skills in identifying part-to-part and part-to-whole relationships, as well as simplifying and interpreting ratios in various contexts.
Ratios vs. Proportions
Ratio and proportion are fundamental mathematical concepts used to express relationships between numbers, quantities, or measures. Both of these terms are often used interchangeably in everyday language, but in mathematics, they have distinct meanings and applications. Understanding their similarities and differences is essential for solving problems related to scaling, comparison, and equivalence.
Similarities
At their core, both ratio and proportion involve comparisons between quantities. A ratio is a comparison between two quantities, while a proportion refers to the equivalence of two ratios. Thus, a proportion is essentially a relationship between two ratios, meaning they share a common foundation in the idea of comparison.
Relationship with Numbers – Both ratios and proportions deal with relationships between numbers, focusing on how one number relates to another in terms of size or quantity. For instance, in the ratio a:b, the comparison between a and b mirrors the concept in a proportion, where a:b=c:d.
Multiplicative Nature – Ratios and proportions are both multiplicative. In a ratio, you can scale both terms (e.g., doubling or halving both numbers in the ratio) without changing the fundamental relationship between the numbers. Similarly, proportions rely on this scaling, as two ratios are said to be proportional if they can be transformed into one another by multiplication or division by the same number.
Applications in Real-Life Situations – Both concepts are widely applied in fields such as physics, economics, engineering, and even art. Ratios are used to compare quantities such as speeds, densities, or financial performance, while proportions are key to maintaining the balance of those ratios, like ensuring consistent scaling in a recipe or model.
Differences
While ratio and proportion are related, they are distinct in terms of their definitions, usage, and mathematical properties. A ratio is simply a way of comparing two numbers. It expresses how much of one quantity exists compared to another. For instance, the ratio of 3 apples to 2 oranges can be written as 3:2 or 3/2. In contrast, a proportion is an equation that shows two ratios are equal. For example, if the ratio of boys to girls in one class is the same as the ratio in another class, it can be written as 3/2 = 6/4, indicating that the two ratios form a proportion.
In terms of function, a ratio is used for direct comparison. It highlights how two quantities relate to each other in a single instance, such as comparing measurements or combining items in a mixture. A proportion, however, goes further by determining whether two ratios are equivalent. This makes proportions useful for solving problems involving scaling or finding unknown values. For example, if two equivalent ratios form a proportion, you can solve for a missing value by maintaining their equality.
Ratios are typically represented using a colon or a fraction, such as a:b or a/b. While they indicate a relationship, ratios alone do not signify equality between quantities. Proportions, on the other hand, are represented by equations where two ratios are set equal to each other, such as a:b = c:d or a/b = c/d. This notation specifically denotes that the two compared ratios are equal.
When solving problems with ratios, you might simplify, compare, or apply them in practical contexts, like scaling quantities. Proportions, however, often involve solving for an unknown value. Given three terms of a proportion, you can use cross-multiplication to find the fourth. For instance, in the proportion a/b = c/d, cross-multiplying gives a x d = b x c, which helps solve for unknowns in proportional relationships.
Mathematically, the interpretation of ratios and proportions differs as well. A ratio represents a single, fixed relationship, such as 3/2, emphasizing the comparison between two quantities without implying equality. A proportion, on the other hand, involves two ratios set equal to each other, indicating a constant rate of change between the quantities being compared. For instance, in the proportion a/b = c/d, an increase in a results in a proportional increase in c, preserving the equality between the two ratios.