Rounding Fractions Worksheets
About These 15 Worksheets
Rounding fractions worksheets are an essential tool in teaching students how to simplify their understanding of fractions by converting them to the nearest whole number or fraction. These worksheets cover a wide range of rounding exercises that help students become proficient in approximating values, a skill that is not only foundational in mathematics but also in real-life situations where exact numbers are less important than estimates. Let’s explore the different types of rounding fractions worksheets and the math skills they impart.
Rounding Proper Fractions to the Nearest Whole Number
In these worksheets, students are presented with proper fractions-fractions where the numerator is less than the denominator-and are asked to round them to the nearest whole number. For example, fractions like 3/4 or 1/2 need to be rounded. The key skill taught here is the ability to assess whether a fraction is closer to 0, 1, or in some cases, even closer to 2, depending on the context of the fraction. Students learn how to compare the numerator to the denominator, understand when a fraction is greater than or less than half, and then make a judgment on rounding up or down. This exercise builds a student’s number sense and helps them intuitively understand the size of fractions in relation to whole numbers.
Rounding Improper Fractions to the Nearest Whole Number
When working with improper fractions, where the numerator is greater than or equal to the denominator, students face a slightly different challenge. These worksheets require students to first recognize that an improper fraction represents a value greater than one whole number. They must then decide whether the fraction should be rounded to the next highest or lowest whole number. For instance, with a fraction like 9/4, students would recognize that it is just over 2 (since 8/4 equals 2), and hence they would round down to 2 or up to 3 depending on the fraction’s proximity to the next whole number. This practice reinforces their ability to work with numbers greater than one and enhances their skills in estimating and rounding more complex values.
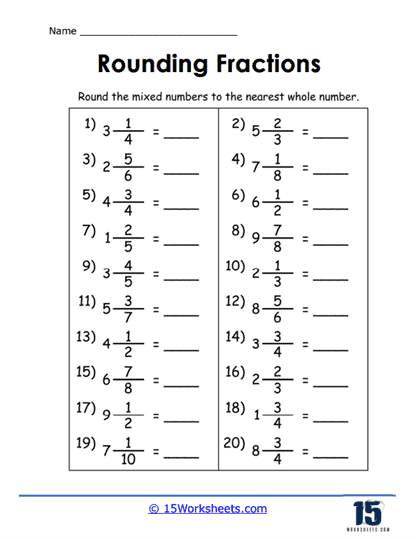
Rounding Mixed Numbers to the Nearest Whole Number
Mixed numbers, which combine whole numbers with fractions, present a unique rounding challenge that these worksheets address. Students learn to first identify the whole number part of the mixed number and then focus on the fractional part to determine whether to round up or down. For example, with a mixed number like 4 3/4, students must decide whether to round to 4 or 5. This type of exercise helps students become comfortable with the dual nature of mixed numbers and strengthens their ability to make decisions based on the fractional part. It also serves as a practical application of the rounding skills learned with proper and improper fractions.
Rounding Decimals to the Nearest Fraction
Rounding decimals to the nearest fraction is another critical exercise found in these worksheets. Here, students work with decimal numbers and learn to approximate them to the nearest fraction, typically to the nearest half or quarter. This skill is particularly useful when students are faced with measurements or data that are presented in decimal form but need to be interpreted in terms of fractions. For instance, rounding 0.33 to the nearest half would help students understand that it’s closer to 1/3, but may be rounded up or down depending on the specific instructions of the worksheet. This exercise deepens students’ understanding of the relationship between decimals and fractions, bridging the gap between these two forms of numerical expression.
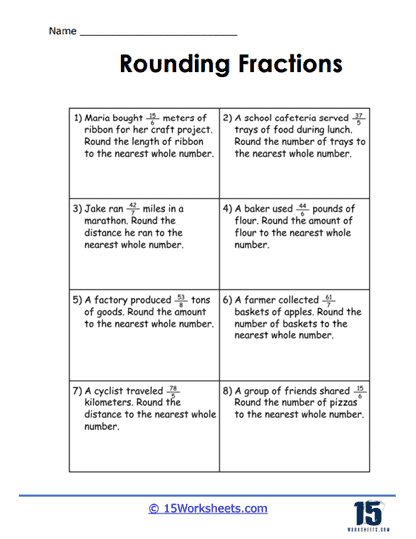
Rounding and Estimating in Word Problems
Word problems that involve rounding fractions to the nearest whole number take rounding exercises to a practical level. In these worksheets, students are presented with real-world scenarios where they must round numbers to the nearest whole number before solving the problem. For example, a problem might ask students to round the number of kilometers a cyclist traveled to the nearest whole number, based on a fractional distance. These word problems not only reinforce the rounding skills students have developed but also teach them how to apply these skills in everyday situations. This type of worksheet is excellent for developing critical thinking and problem-solving skills, as students must interpret the problem, decide how to round the numbers, and then carry out the necessary calculations.
Rounding Repeating Decimals to the Nearest Fraction
Repeating decimals, such as 0.333… or 0.666…, can be challenging for students to round, but these worksheets provide the practice necessary to master this skill. Students are asked to round repeating decimals to the nearest fraction, often to the nearest third or sixth. This exercise requires students to understand the concept of infinite decimals and how they relate to fractions. It also helps solidify their grasp of equivalent fractions, as they learn that 0.333… is equivalent to 1/3 and 0.666… is equivalent to 2/3. This type of rounding worksheet is particularly useful in preparing students for more advanced mathematical concepts involving decimals and fractions.
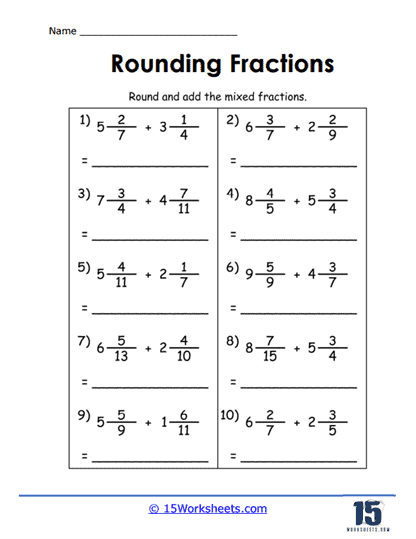
Rounding and Adding Mixed Fractions
A more complex exercise involves rounding mixed fractions and then adding them together. In these worksheets, students first round each mixed fraction to the nearest whole number and then perform addition on the rounded figures. For example, students might be asked to round 2 3/7 and 4 5/9 before adding them together. This exercise helps students develop multi-step problem-solving skills, as they must accurately round each mixed number before proceeding with the addition. It also reinforces their understanding of both rounding and basic arithmetic operations, making it a valuable tool for comprehensive math practice.
Identifying Fractions Greater Than Half
Some worksheets focus on helping students identify which fractions in a given list are greater than half. This type of worksheet sharpens students’ comparative skills, as they must evaluate each fraction and determine its size relative to one-half. For example, students might be given fractions like 2/5, 3/4, and 1/6 and asked to select the ones that are greater than 1/2. This exercise is crucial for developing a deep understanding of fraction comparison, an important skill in many areas of math, including ratio and proportion, probability, and more.
Skills Developed Across All Worksheets
Across all these worksheets, several key mathematical skills are developed and reinforced. First and foremost is the concept of number sense, which is the ability to understand, interpret, and work with numbers comfortably. Rounding exercises strengthen students’ number sense by requiring them to make judgments about the relative size of numbers and their proximity to benchmarks like whole numbers or simple fractions.
Another important skill is estimation. By rounding fractions and decimals, students learn how to approximate values, which is essential for making quick calculations and solving problems where precision is not necessary. Estimation is a critical life skill, useful in everything from shopping and budgeting to measuring and cooking.
These worksheets also improve students’ ability to work with fractions and decimals, two areas that are often challenging for many learners. By providing repeated practice in rounding, these exercises help demystify fractions and decimals, making them more accessible and easier to work with. Students become more comfortable converting between different forms of numbers, such as turning a decimal into a fraction or understanding how a mixed number can be simplified by rounding.
The worksheets promote problem-solving and critical thinking. Whether students are rounding fractions in word problems or determining which fractions are greater than a half, they must engage their problem-solving skills to arrive at the correct answers. This process encourages logical thinking and the ability to follow a multi-step procedure, both of which are essential in higher-level math and everyday situations.