Mayan Numbers
Worksheet Description
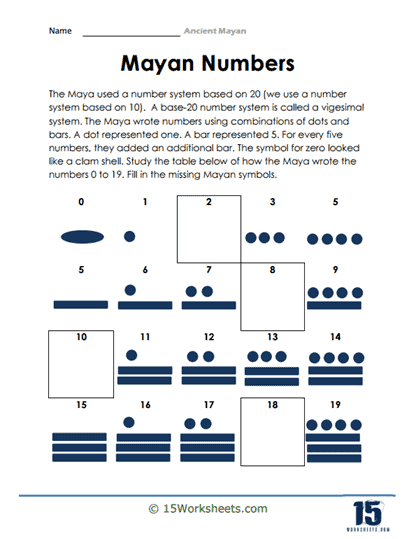
The Maya used a number system based on 20 (we use a number system based on 10). A base-20 number system is called a vigesimal system. The Maya wrote numbers using combinations of dots and bars. A dot represented one. A bar represented 5. For every five numbers, they added an additional bar. The symbol for zero looked like a clam shell. Study the table below of how the Maya wrote the numbers 0 to 19. Fill in the missing Mayan symbols.
This worksheet delves into the numerical system of the Ancient Mayan civilization, emphasizing its vigesimal (base-20) nature, in contrast to the base-10 system prevalent today. It illustrates how the Mayans represented numbers using dots and bars, where a dot signifies one and a bar denotes five. Moreover, it highlights the Mayan symbol for zero, which bears resemblance to a clam shell. The task presented to students involves filling in the missing Mayan symbols for the numbers provided, using the given chart as a reference.
To master this skill, students must first understand the basic principles: a dot represents a single unit, and a bar signifies five units. Starting from the number one, they should practice drawing the Mayan symbols up to 19, recognizing patterns as the numbers increase. For instance, after reaching four dots (representing the number four), the fifth dot is replaced by a bar to symbolize the number five. As the numbers progress, additional bars and dots are added, ensuring that no more than four dots or three bars are used for numbers up to 19.
The primary goal of this worksheet is to familiarize students with the Mayan numerical system, offering insight into the cultural and mathematical practices of the civilization. It encourages students to think outside the conventional base-10 system, promoting flexibility in understanding different numeral systems. By engaging in this exercise, students not only learn about Mayan mathematics but also hone their skills in pattern recognition and problem-solving. This worksheet serves as a bridge connecting historical knowledge with practical application, illustrating the universality and diversity of mathematical representation throughout human history.
